Example 1: A uniform rod of mass m and length l is on a smooth horizontal table (friction = 0) and is hit at one of its ends so that an impulse J is imparted to it in its perpendicular direction (see figure 5). What is its subsequent motion?

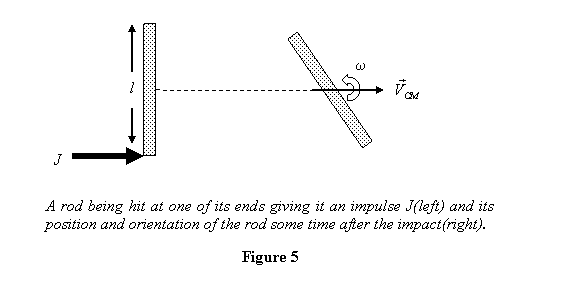
As the rod is hit, its CM will start moving with a velocity

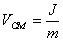
At the same time the rod also starts rotating. Although the CM will be accelerating during the impact, we can apply the angular momentum-torque equation about it with only external torque in the equation. If the angular speed of the rod after the impact is ω, it is given by

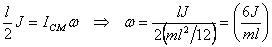
Note that in the sentence above, I have said 'angular speed of the rod' and not 'angular speed of the rod about the CM because the sense and amount of rotation about any point in the body is the same, as was discussed in a previous lecture. The position and orientation of the rod some time after the impact is also shown in figure 5.

Example 2: A wheel of mass m and radius R is sliding on a smooth surface (No rolling) with speed V. It then hits a very rough surface so that it starts rolling (see figure 6). What is it rolling speed?

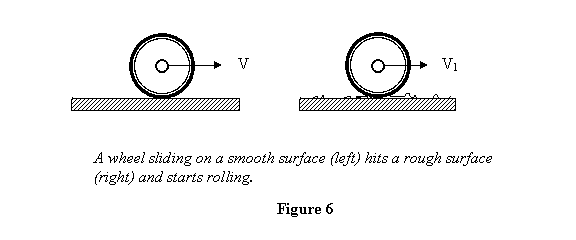
Let the rolling speed of the wheel be V₁ . As soon as the wheel hits the rough surface, it gets an impulse J at its point on the surface in the direction opposite to its velocity. This reduces its speed and also makes it rotate. It rolls if the speed V₁ of its CM is equal to ωR , where ω  is the rolling speed it gains after hitting the rough surface. The change in the CM speed is given by

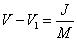
Applying the angular-momentum torque equation about the CM, we get

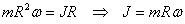
With the condition of rolling, 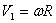, the above two equations give

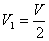
I would like you to repeat the same exercise for a disc.

The problem can also be solved by applying conservation of the point of impact on ground, because the impulse gives zero torque about that point. The initial angular momentum of the wheel with respect to that point is mVR . The final angular momentum is (angular momentum of the CM plus angular momentum about the CM). This comes out to be (mV₁R + mR²ω) . Equating this to mVR and using the rolling condition gives the same answer as above. A warning: keep in mind that the torque is being taken with respect to the point on ground and not the point on the wheel that is touching the ground. Doing that will not be correct because at the time of impact the point on the wheel is accelerating in the direction opposite to .

I now solve a problem that involves, in addition to the equations above, energy conservation also.

Example 3: A rod of mass m and length l is held making an angle Φ from the horizontal at a height h from the floor (see figure 7). When dropped from rest, what will be its linear and angular speed after it rebounds from the floor? Assume no energy is lost during the impact with the floor.

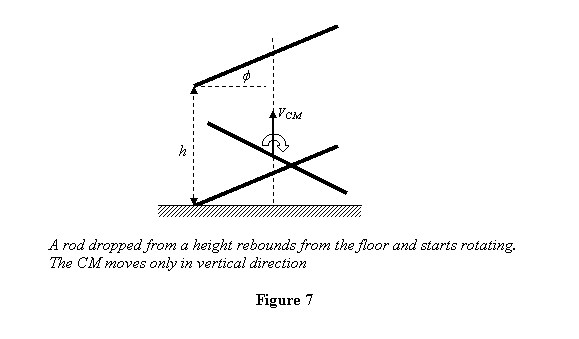
When the rod hits the floor, it receives an impulse J from the ground in the vertically up direction. Although the rod is also being acted upon by its weight, we neglect its effect during impact (see discussion in the lecture on momentum). Since all the forces are in the vertical direction, the CM of the rod also moves only vertically. Before hitting the floor, the speed of the CM is 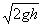and the angular speed of the rod is zero. Let the rebound speed of the CM be V and the angular speed of the rod after rebounding be ω. Then similar to the example above, these quantities are related as (keep in mind that we are dealing with vector quantities so their signs have to be properly accounted for)

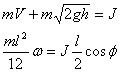
These are two equations for three unknowns: V, ω  and J. We therefore need one more equation. This is provided by energy conservation. We express the kinetic energy of the rod after it rebounds as the sum of the kinetic energy of its CM and the kinetic energy about its CM. Thus immediately after the impact, energy conservation gives

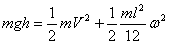
Now we have three equations that can be solved for the three unknowns. This is left for you to do.

Question you might now ask is if we could use the principle angular momentum and energy conservation directly to solve this problem in a manner similar to what we did at the end of the last example. We would like to apply the conservation of angular momentum about the point of impact on the ground because torque due to the impulse about this point vanishes. Although there is another external force - the weight of the rod - acting on the system, its effect during the impact can be ignored because very short duration of impact. Thus we can say that the angular momentum about the point of impact is conserved. This gives (left as an exercise for you)

This is the same equation that is obtained by combining the first two equations above. Thus we obtain the same answer by this method also.

I end this lecture by giving you an exercise.

Exercise: A disc of mass m and radius R is made to roll on a rough surface by applying a force F at its centre. If it does not slip on the floor, i.e. it does pure rolling, find its acceleration by applying methods developed in this lecture.