Rotation
of a rigid body combined with translation of the
axis parallel to itself:
Let us now introduce
translation of the rotational axis parallel to itself
- it may even accelerate - and ask what kind on motion
is going to follow. So for example there may be a
rod on a horizontal table and is hit by an impulse
one end, and we may be interested in its subsequent
motion. I general it could be a rigid body of general
shape on which we apply a force. We split the motion
into a translation of the CM of the body and rotation
about an axis passing through the CM. By doing so
the equation of motion for the translational motion
of the CM is very easy. It is
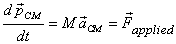
Here 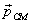 is
the total momentum of the body; M is its mass; is
the total momentum of the body; M is its mass; 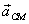 the
acceleration of the CM and the
acceleration of the CM and 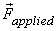 the
total applied force. With this equation we know how the
CM of the body translates. Next we wish to find the rotation
of the body with respect to an axis passing through the
CM (recall that the most general motion of a rigid body
is translation of a point and rotation about that point).
But the question is: can we apply the
total applied force. With this equation we know how the
CM of the body translates. Next we wish to find the rotation
of the body with respect to an axis passing through the
CM (recall that the most general motion of a rigid body
is translation of a point and rotation about that point).
But the question is: can we apply
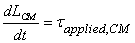
where 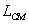 is
the angular momentum about the CM and is
the angular momentum about the CM and 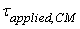 is
the applied torque about the axis of rotation passing
through the CM. I raise this question because in general
the CM will also be accelerating and therefore with respect
to the CM, there will be a fictitious force that may
also give rise to a fictitious torque which is in addition
to the applied torque is
the applied torque about the axis of rotation passing
through the CM. I raise this question because in general
the CM will also be accelerating and therefore with respect
to the CM, there will be a fictitious force that may
also give rise to a fictitious torque which is in addition
to the applied torque 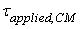 .
However, it is easy to see that such a fictitious torque
about the CM will always be zero. This is because the
fictitious force effectively acts at the CM itself. Because
of this reason, there is one more point about which the
torque due to the fictitious force vanishes: this is
the point that accelerates towards the CM. Thus the equation
above can be applied safely about these two points. There
is also a third point about which the above equation
is valid. This is the point that does not accelerate
at all. Let me now prove these statements. .
However, it is easy to see that such a fictitious torque
about the CM will always be zero. This is because the
fictitious force effectively acts at the CM itself. Because
of this reason, there is one more point about which the
torque due to the fictitious force vanishes: this is
the point that accelerates towards the CM. Thus the equation
above can be applied safely about these two points. There
is also a third point about which the above equation
is valid. This is the point that does not accelerate
at all. Let me now prove these statements.
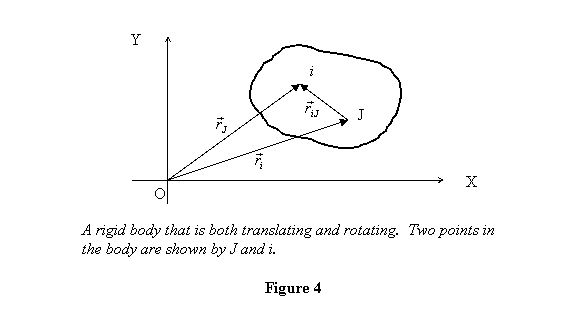
Shown in figure 4 is a rigid body performing a general
motion, i.e. it is both translating as well as rotating.
For convenience we have shown the body in two dimensions.
Two points J and i of the body are
also shown. These points are also moving with the body.
We now calculate the rate of change of the angular momentum
about point J . This is done below.
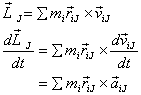
where all the terms have their standard meaning and the
subscript (iJ) denotes the quantity being
calculated for point i with respect to point J .
Denoting the velocity and acceleration of point i about
the origin O as 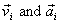 ,
respectively, and that of J as ,
respectively, and that of J as 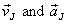 ,
we have ,
we have
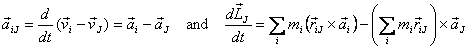
With 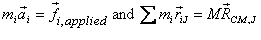 ,
where ,
where 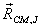 is
the position vector of the CM with respect to J ,
we get is
the position vector of the CM with respect to J ,
we get
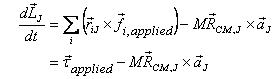
If we want the rate of change of the angular momentum
to depend only on the applied torque calculated about
J, we should have
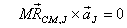
That will happen under the following three conditions:

I have just shown you that irrespective of the whether
point J is accelerating, rotating or performing
some general motion, the equation
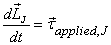
can be applied about J if it satisfies one of
the three conditions obtained above. Notice that in under
these conditions the right-hand side has only the externally
applied torque. Thus if we choose one of these points
to apply the angular momentum-torque equation, we do
not have to worry about any fictitious torques arising
because we are sitting on an accelerating point. We have
been applying the angular momentum-torque equation about
points satisfying condition I above; it includes
stationary points also. Of the other two points, it is
always safer to apply the equation about the CM (condition II ).
This is because of the difficulty in ensuring that a
point is accelerating towards the CM (condition III ),
although in some situations it may be easy. We will discuss
one such case below. We now solve some simple examples
to illustrate what we have learnt above.
|