Lecture 20
Rigid body dynamics III: Rotation and Translation

We have seen in the past two lectures how do we go about solving the rigid body dynamics problem by considering the rate of change of angular momentum. In the previous lecture, we concentrated on rotation about a fixed axis and solved problems involving conservation of angular momentum about that axis. In this lecture we consider what happens where an external torque is applied and also when the axis is allowed to translate parallel to itself.

Let us first take the case when the axis is stationary and a torque is applied. Take for instance your pen or a scale and hold it lightly at one of its ends so as to pivot it there. Raise the other end so that the scale is horizontal and then leave it. You will see that the scale swings down. I would like to calculate the speed of its CM when the scale is vertical after being released from horizontal position (see figure 1). Assume that there is no loss due to friction. In this case I will solve this problem in two ways and also comment on a wrong way.

I take the mass of the scale to be m and its length l. Then its moment of inertia about one of its ends is .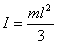

I first solve the problem using energy conservation. Since there is no loss due to friction the total mechanical energy is conserved. Therefore the total mechanical energy is conserved. Let us take the potential energy to be zero when the scale is horizontal. Since the scale starts with zero initial angular speed, its total mechanical energy is zero. When the scale reaches the vertical position, its CM has moved down by a distance 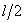so its potential energy is . 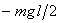If its angular speed at that position is ω, then by conservation of energy

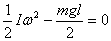
which gives

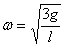
I now solve the problem by a direct application of torque equation. When the scale makes an angle θ from the horizontal (see figure 2), the torque on it is given as

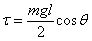
The angular momentum-torque equation then gives

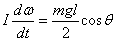
Substituting 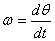and the value of I from above this leads to

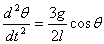
This equation cannot be integrated with respect to time directly. Recall from the proof of work-energy theorem that in such situations we change transform the equation to write it in terms of the displacement variable, which is the angle in this case. So we write

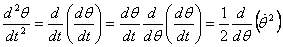
to write the equation above as

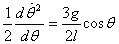
Integrating this equation then gives

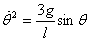
For 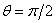this gives the same answer as obtained earlier. If you have noticed, what we have done here is actually used the work-energy theorem

You may ask at this point: wouldn't the correct way of solving this problem be to equate the kinetic energy of the CM to the change in the potential energy. This would lead to

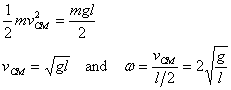
The reason why this answer is incorrect is the following. Recall from our previous lecture that the most general motion of a rigid body is a translation plus a rotation. So while it is true that the CM is moving, the scale is also rotating at the same time. We represent the combination of the two motions as a translation of the CM and a rotation about an axis passing through the CM. Why we split the motion of the scale as a combination of the translation of its CM and a rotation about the CM - and not that of any other point in the body - will be discussed in detail below. For now it is sufficient to say that by doing so the kinetic energy can be written conveniently as (KE of the CM plus KE about the CM). So the true K.E of the scale is

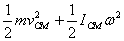
where 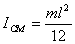is the moment of inertia about the CM. Using the relationship 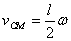  this gives the same kinetic energy as that used above in applying the energy conservation method. This correct approach then gives the same answer as obtained above.

An interesting problem related to the one solved above is as follows. Sometimes if a book you are holding slips out your hand, it usually falls with its upper face down (see figure 3). You can try this at home and see for yourself. In fact there is an interesting book which has a title based on this observation. It is entitled "Why toast lands jelly side down" and is authored by Robert Ehrlich (Universities press, Hyderabad 1999). Let us try to understand this observation.

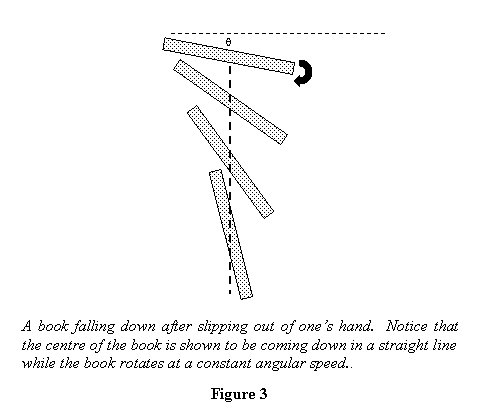
When the book falls its angular acceleration α immediately after it slips off the hand is calculated approximately as given below

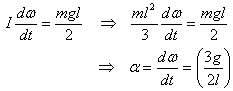
Here m is the mass of the book and l its length. I call it an approximate expression because in our calculation we have assumed the book to be in horizontal position. It will slip off w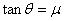hen   or for small angles θ ~ µ, where m is the coefficient of friction between the book and the hand. Starting with zero initial angular speed, let the angular speed of the book when it slips out of the hand be ω . Then

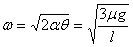
Taking µ = 0.5, g = 10ms^{- 2} and l = 20cm = 0.2m , we get

ω = 8.7 rad s^{- 1}

After the book has come out of the hands, there is no external torque on it about its CM so it falls rotating with a constant angular speed of about 8.7rad s^{- 1}. Keep in mind that the sense and amount of rotation of a rigid body is the same irrespective of the point about which its rotation is considered. So although before slipping out of the hand, I did the calculation for its angular speed taking its edge on the hand as the axis, after it comes out of the hand, I consider its motion as the translation of its CM and rotation about its CM. Let us stake a typical height of about 1m from which the book falls. Then the time it takes to reach the ground is

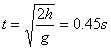
Thus the angle through which the book rotates by the time it reaches the ground is

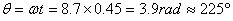
If we add to this angle the initial rotation of θ = µ = 0.5, the angle increases to about 250°. The angle of rotation of course varies in a range but it is around 180°.You see that the book has just the right angular speed and the time of fall for it to turn by around 180°. That is precisely what we observe.