Lecture 19
Rotational dynamics II: Rotation about a fixed axis

We saw in the previous lecture on rigid bodies that a rigid body in general requires six parameters to describe its motion, and the dynamic of a rigid body is determined through its angular momentum 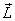that satisfies the equation 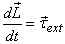, where 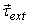is the applied torque on the body. Further, 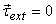means that is a constant.

In this lecture I start with an example of the conservation of angular momentum involving two particles. I again show that a direct application of Newton 's laws and a solution through the conservation of angular momentum give the same answer.

 

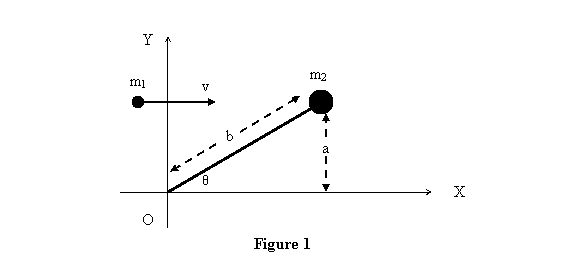
Example 1: There is a rigid massless rod of length b held at point O carrying a mass m₂ at its other end. Let the y-coordinate of m₂ be a. Another mass m₁ comes parallel to the x-axis and hits m₂ and the two masses get stuck together (see figure 1). Question is at what speed will the rod rotate?

Let us apply the conservation of angular momentum to the system of two masses about point O. This is because the only external force acts at O so the torque about O is zero and therefore the angular momentum about O is conserved. Since the particles are moving in the xy plane, their angular momentum is going to be in the z direction. So we write the unit vector explicitly and work in terms of numbers (both positive and negative) only. Assume that the angular velocity of the rod after the mass m₁ gets stuck with it is ω. To apply angular momentum conservation we calculate the angular momentum of the system before and after collision and equate them.

Initial angular momentum about O = m₁ va

Final angular momentum = (m₁ + m₂ )b² ω

Equating the two gives

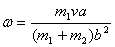
Let us now see if the conventional force analysis also gives the same answer. The incoming mass m₁ comes in with momentum m₁v. Now after m₂  is hit, it cannot have any movement parallel to the rod because the rod is rigid, i.e. the rod is capable of generating enough tension (impulse) in it to make the component of momentum parallel to the rod zero. On the other hand, there is no force perpendicular to the rod so the momentum component p in that direction remains unchanged after the hit. Now

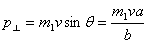
After the masses get stuck together, p 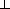remains the same. Thus the new speed v' acquired by the masses will be such that

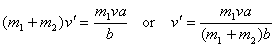
This gives

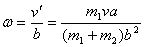
which is the same as obtained by angular momentum conservation. Thus again showing the equivalence of the two methods.

With all this preparation, let us now start with the simplest motion of a rigid body that is the rotation of a rigid body about an axis fixed in space. So the axis is neither translating nor rotating. Without any loss of generality, let us call this axis the z-axis. In this case the body has only one degree of freedom and the only variable that we need to describe the motion of the body is the angle of rotation about the axis. Further, the only relevant component of angular momentum in this case is the component along the z-axis. Note that there may be other components of angular momentum but their change is accounted for by torques applied on the axis to keep it fixed in space. Calculation of such torques will be discussed in later lectures. Suffices here is to say that these torques arise out of the constraint forces that enforce the constraint of the axis being fixed in space.

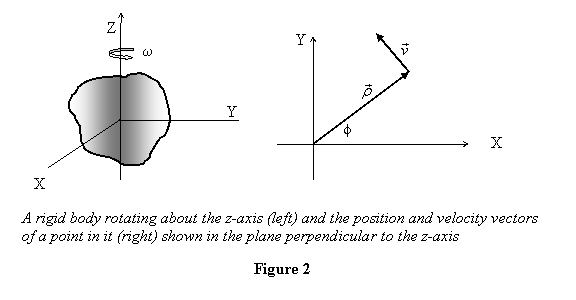
Shown in figure 2 is a rigid body rotating about the z-axis with an angular speed ω. Also shown there is the position and velocity vector of one of its constituent particles of mass m_i in a plane perpendicular to the rotation axis. We wish to calculate the z component of the angular momentum.

The z component will be given as

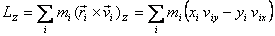
For a particle at distance ρ_i from the z-axis and its radius vector making an angle Φ_i from the x-axis

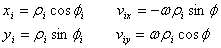
so that

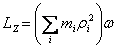
Calling 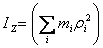the moment of inertial about the rotation axis, we can write

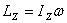
Depending on the direction of ω, angular momentum about an axis could have negative or positive values because it is a vector quantity. The convention we take is the right-hand convention; Let the thumb of one's right hand point in the positive z direction; if the rotation of the body is in the same (opposite) direction as the fingers, ω is positive (negative).

Having defined the moment of inertia about an axis, we make a few comments on it. First thing we notice about it is that it depends on the perpendicular distance of point masses from the axis of rotation. So no matter where we take the origin of the coordinate system, the moment of inertia of a rigid body about an axis is always going to be the same. Secondly, for continuously distribute mass moment of inertia is calculated as the integral

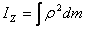
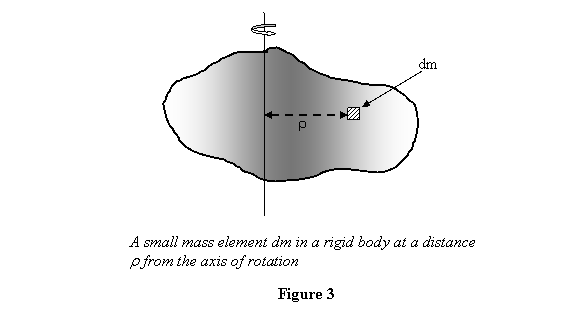
where ρ is the perpendicular distance of a small mass element dm taken in the body (see figure 3).

Finally, for planar objects the moment of inertia is the same as the second moment of an area except that the area is replaced by the mass.

We now calculate moment of inertia of some objects.