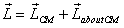After this initial demonstration of 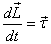with a single particle, we move on to a system of many particles. It is really a system of many particles that we are dealing with in rigid-body dynamics.

Angular Momentum of a collection of particles: If there are many particles then the total angular momentum 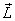about a point O is the sum of individual angular momenta of each particle about O . Thus

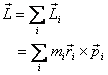
As for the angular momentum of a single particle, the angular momentum of a many-particle system is also origin-dependent. (Question: Under what conditions will the angular momentum be independent of the origin?)

Now recall that the kinetic energy for a collection of particles is the sum of the kinetic energy of their centre of mass (CM) and the kinetic energy of particles with respect to the CM. Interestingly the angular momentum of a many-particle system can be expressed in the same manner. Thus the total angular momentum of a collection of particles is equal to the angular momentum of the CM plus the angular momentum of particles about the CM. Let us now prove it. To do so express the position vector and the velocity of a particle as

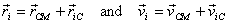
where 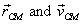refer to the position and velocity of the CM and 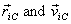the position and velocity of i^th particle with respect to the CM. Now the total angular momentum can be writes as

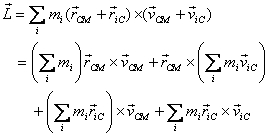
However, by definition of the CM, . Therefore the second and the last term in the expression above do not contribute. The remaining terms are written as

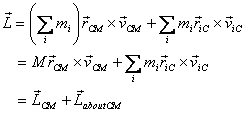
where M is the total mass of the system. This is a remarkable result, and as we will see, facilitates calculations involving rigid-body dynamics a lot. Keep in mind though that this result is true only with for the CM. For an arbitrary point O' in the body, we cannot write

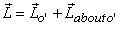
because 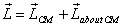depends explicitly on the definition of the CM. We will later use this fact to obtain the parallel axis theorem that you may have learnt in your previous classes. The theorem is similar to the transfer theorem of the second-moment of an area.

The relationship 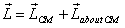also tells us that if the total momentum of a system of particles is zero, its angular momentum will be independent of the origin. I leave the simple proof for you to work out.

Example: Take a bicycle wheel of radius R rolling along the ground and assume all its mass M is concentrated along the rim. If it is rolling without slipping then its motion is as follows: its CM moves with speed V along a straight line and the wheel rotates about the CM with angular speed 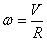so that the point on ground is at rest. We want to find its angular momentum in a frame stuck to the ground such that the wheel is moving along its x-axis see figure 9).

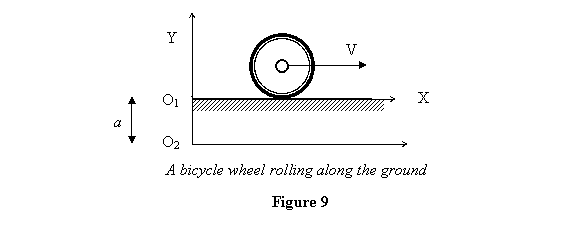
The angular momentum of the wheel about its CM is given as

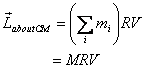
So angular momentum about the origin O₁ (see figure 9) would be

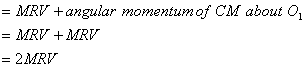
On the other hand, if we were to calculate the angular momentum about O₂ (see figure 9) it would come out to be

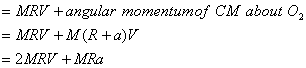
Notice that in both the cases we have added the angular momentum of the CM and that about the CM. It is because their directions come out to be the same (negative z direction). One must be careful about these things because angular momentum is a vector quantity. Having introduced you to the concept of angular momentum, I now discuss about the rate of its change for a many-particle system where the particles are interacting with each other also.

 

Dynamic of a rigid body; 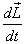and conservation of angular momentum: Let us now look at 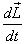in the case of a collection of particles which are interacting with each other and are also being acted upon by external forces.

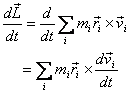
But 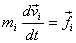( 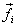s the total force, i.e. the sum of external and internal forces on the particle). This gives

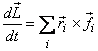
Before simplifying this equation in terms of the external torque, let us see where does this equation lead us for a two particle system shown in figure 10?

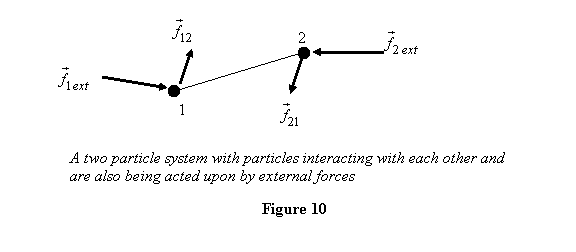
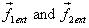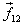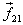The two particles 1 and 2 shown in figure 10 are external forces , respectively. They also interact with each other with particle 2 applying a force on particle 1 and particle 1 applying a force on particle 2. We assume the forces to be following Newton 's III^rd law so that 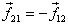. Now the rate of change for this system can be written as

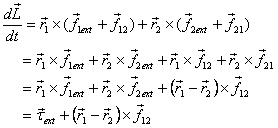
Thus the rate of change of angular momentum is equal to only the external torque if 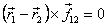or 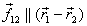,i.e. the force between the particles is along the line joining them. At this point I would like you to recall that in the case of linear momentum, the rate of change on linear momentum equals the total external force, i.e. 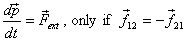. For angular momentum to satisfy , the additional condition of 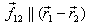is also needed. Fortunately for most of the mechanical applications this is true. Let us now generalize this to the case of a many-particle system. For such a system

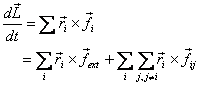
Recall the trick used in the case of linear momentum that

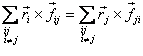
so that

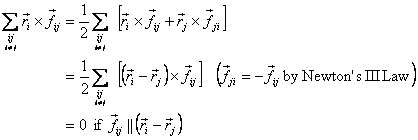
Under these conditions, i.e. if the force between the particles is along the line joining them , we get

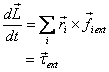
Thus if 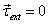then 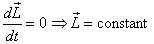. Thus is the law of conservation of total angular momentum. In the next lecture we will do a few example of its application.

 

We now conclude this lecture by listing the following points that we have learnt:

1. A rigid body needs six parameters to describe its general motion; three for translation and three for rotation,
2. Dynamics of rigid body is governed by its angular momentum,
3. The angular momentum satisfies the equation

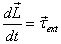
under the condition that the internal forces satisfy Newton 's III^rd law and an additional condition that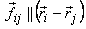

4.