For simplicity, in the beginning we are going to focus
on rigid moving with its one point fixed. Thus it will
change only by changing its orientation. We will further
simplify the problem by considering rotation about an
axis fixed in space. In the next step, we will allow
the axis to translate but without changing its orientation.
Finally we will also let the orientation of the axis
change. Thus we will increase the complexity of the problem
gradually.
Dynamics of rigid body: The
dynamics of a rigid body is best described by considering
its angular momentum. You can think of angular momentum
as the rotational counter part of linear momentum. This
quantity is central to describing rotational motion of
a rigid body. So let us first spend some time in understanding
this quantity. Although we are introducing angular momentum
here in the context of rigid bodies, the treatment below
is quite general.
For a single particle moving with linear
momentum 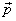 at
a distance at
a distance 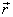 from
the origin the angular momentum from
the origin the angular momentum 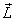 is
defined as is
defined as
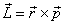
You can immediately see that it is an origin-dependent
quantity. If we calculate it with respect to some other
point, it will come out to be different. If a particle
of mass m is moving in a plane then using the
polar coordinates for it, it is easily shown that its
angular momentum is 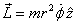 .
Let us now find out what is the rate of change of angular
moment? It is calculated below. .
Let us now find out what is the rate of change of angular
moment? It is calculated below.
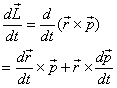
With 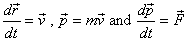 ,
where ,
where 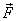 is
the force on the particle, the equation above is simplified
to is
the force on the particle, the equation above is simplified
to
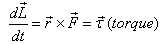
Thus rate of change of angular momentum is equal to the
torque applied on the body. From the equation above,
the law of conservation of angular momentum follows
immediately: If the applied torque 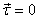 the
angular momentum the
angular momentum 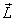 does
not change, i.e. it is a constant. The equation does
not change, i.e. it is a constant. The equation
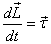
is the angular momentum equivalent of Newton 's IInd
law. Let us now illustrate the ideas presented so far
with the example of a conical pendulum.
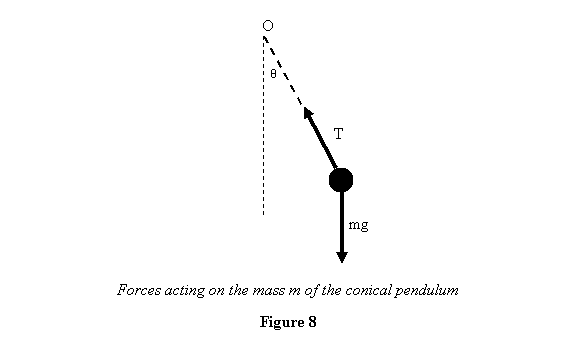
Example 1: A conical pendulum is like
the regular pendulum with a light (mass m = 0 )
rigid rod carrying a bob of mass m at one of
its ends. The other end is fixed and the bob moves in
a circle with speed v (see figure 6). We wish
to calculate the tension in the rod and the angle θ it
makes from the vertical by applying the angular momentum-torque
equation.
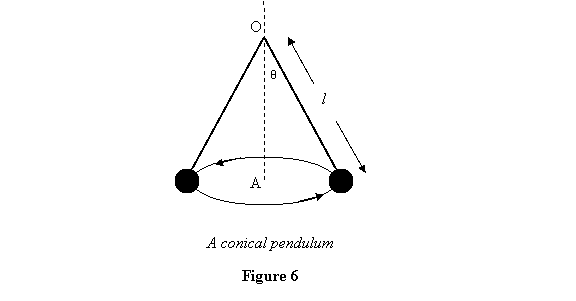
Let us first calculate angular momentum about point O .
We will use cylindrical co-ordinates because of the symmetry
of the problem. With respect to O
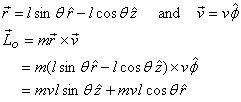
The  vector
looks as shown in figure 7, when the bob of the pendulum
is in the paper plane. vector
looks as shown in figure 7, when the bob of the pendulum
is in the paper plane.
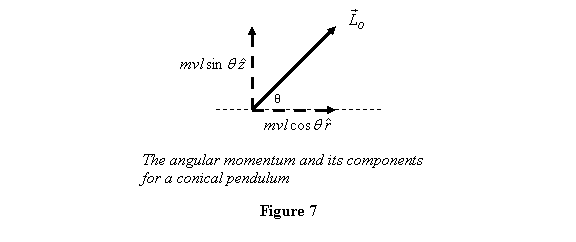
So
the angular momentum 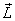 is
perpendicular to the rod (take the dot product with is
perpendicular to the rod (take the dot product with 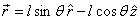 for
mass m and see for yourself) and as the particle
rotates the horizontal component of for
mass m and see for yourself) and as the particle
rotates the horizontal component of 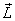 are
rotates with it and the vertical component remains a
constant. Let us now apply the equation are
rotates with it and the vertical component remains a
constant. Let us now apply the equation
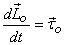
We have

We now calculate the torque acting on the pendulum. There
are two forces, the tension 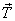 and
the weight and
the weight 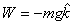 ,
acting on the particle as shown in figure 8. ,
acting on the particle as shown in figure 8.
But  passes
through O and does not give any torque. Thus passes
through O and does not give any torque. Thus
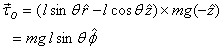
Substituting these in the angular momentum-torque equation 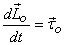 then
gives then
gives
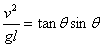
The angular momentum-torque equation therefore gives us
the angle θ that the pendulum makes with the
vertical. How do we find the tension T ? On
the other hand, applying Newton 's second Law we get
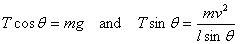
giving
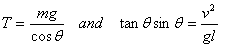
These equations give us both T and θ,
but the equation 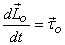 gives
only the angular relationship. Does this mean that the
angular-momentum torque equation is not equivalent to
Newton 's second law? The answer is that it is. It so
happens that in applying the equation about O,
when cross products gives
only the angular relationship. Does this mean that the
angular-momentum torque equation is not equivalent to
Newton 's second law? The answer is that it is. It so
happens that in applying the equation about O,
when cross products 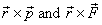 are
taken, some components of the force do not contribute
to the torque and drop out of the equation. For example
in this case are
taken, some components of the force do not contribute
to the torque and drop out of the equation. For example
in this case 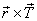 becomes
zero. To get full solution, therefore, we now apply becomes
zero. To get full solution, therefore, we now apply 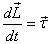 about
point A. Taking A as the origin we have about
point A. Taking A as the origin we have
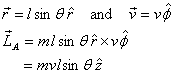
Since all the quantities in 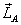 are
constants, we have are
constants, we have
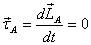
Let us calculate the torque 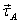 about
A. With A as the origin, the forces are given as about
A. With A as the origin, the forces are given as
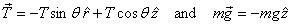
Therefore
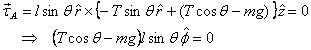
which gives
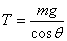
Thus applying 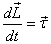 about
two different points gives exactly the same solution
as that obtained from about
two different points gives exactly the same solution
as that obtained from 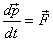 .
Thus the two ways of solving the problem are equivalent.
Through this example I have shown you (a) the origin
dependence of .
Thus the two ways of solving the problem are equivalent.
Through this example I have shown you (a) the origin
dependence of  , and
(b) equivalence of , and
(b) equivalence of  and and 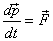 . .
Let me now illustrate conservation of angular momentum
by a well known example: that of Kepler's Law of equal
area concept in equal time. Accordingly, when planets
are going around the sun, the rate at which their position
vector from the sun sweeps the area is a constant. Recall
from the lecture on polar coordinates that for a particle
moving under a radial force, we had obtained that 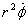 is
a constant. This is nothing but two times the rate of
area sweep by the radius vector. We now want to get this
law from the conservation of angular momentum. is
a constant. This is nothing but two times the rate of
area sweep by the radius vector. We now want to get this
law from the conservation of angular momentum.
For a planet, we know that the force is in redial direction.
So that the torque
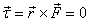
Thus
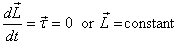
Since 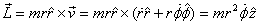 ,
its constancy means ,
its constancy means
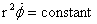
which is Kepler's second law.
|