Lecture 18
Rotational dynamics I: Angular momentum

So far we have applied Newton's laws to point particles and the CM motion for a collection of particles. We are now going to look at what happens beyond the motion of the CM, which is described by the equation

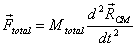
Let us see what else could happen to a body made up of a collection of particles where forces are applied at each point (figure 1). The particles are connected with flexible attachments shown as lines.

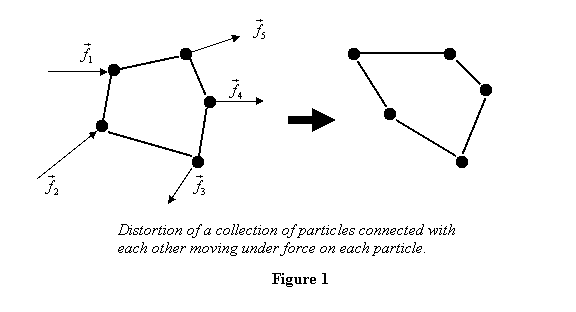
In the figure above, although the CM moves with 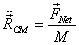, the body itself could deform and change its orientation. Thus the distances between the particles and the angles between lines joining them would change. This is the most general motion that could take place. In the next few lectures we want to focus only one of the effects of the force applied. We are going to assume that a body only changes its orientation but does not deform. This is achieved by keeping the distance between any two particles of the body unchanged. Such a body is known as a rigid body . Thus in the example above, if we connect all the particles with each other by rods of fixed length, the body will become rigid. This is shown in figure 2.

The only possible motion of such a body is a translation plus a change in its orientation. The simplest example of a rigid body is two masses attached at the ends of a rod of fixed length. On the other hand, a tin-can partially filled with sand is not a rigid body since the distance between two particles keeps on changing with the motion of the can.

As stated above, the most general motion of a rigid body is its translation plus its change of orientation. The latter is equivalent to a rotation about a point. The beauty of this decomposition is that to get the final position of the body, we can translate any point in the body and then rotate the body about that point. Irrespective of which point we choose, the sense and the angle of rotation is always the same. Usually this point is taken to be the CM for reasons that will become clear later lectures. This general motion is shown below in figure 3, giving two possible ways of translating and rotating the body.

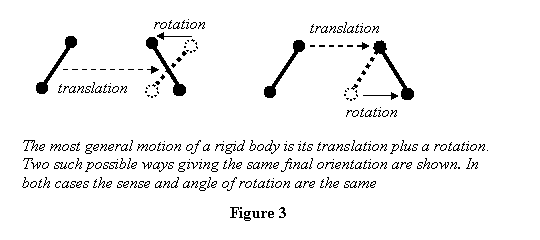
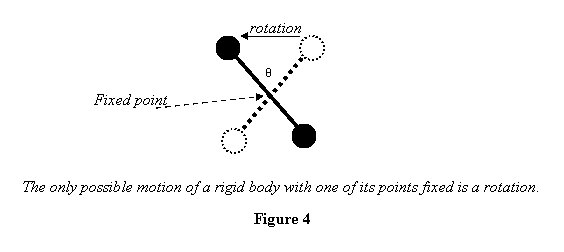
You see that in figure 3 the rigid body has translated and also rotated. On the other hand, if we keep one of the points on the body fixed the only thing the body can do is to change its orientation (see figure 4). Thus with a point fixed, the only possible motion of a rigid body is a rotation.

A question that arises now is how many variables do we need to specify the general motion of a rigid body. It requires three variables - x, y and z coordinates of the point that is translated - to describe the translation, and three more - angle of rotation about each axis - to represent the rotation. You can see that in general a rigid body would require six variables to describe its motion. However, if one of its points is fixed, three variables are sufficient to specify its rotation. So we conclude a rigid body needs six parameters to describe its motion.