Now we consider a two-particle elastic collision in a plane and analyze it. This could be the collision of a striker and a coin on a carom board, for example. It is a two-dimensional case. We are going to analyze the motion graphically. First we look at the velocities in the CM frame. If we take the initial direction of particle 1 towards +x , the velocities of the two particles before and after collision can be shown as done in figure 5. Keep in mind that in an elastic collision, the magnitude of the velocities of each particle remains unchanged in the CM frame. However the direction of the velocity for each particle changes by an angle Θ_CM. as shown in figure 5.

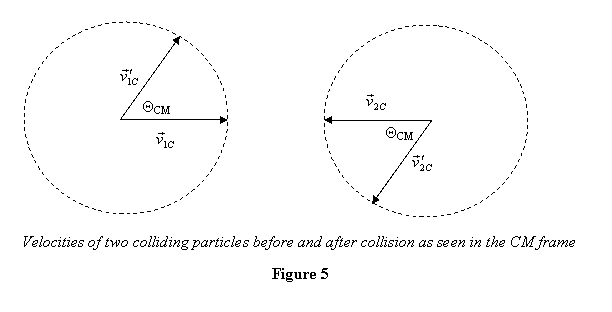
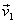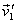The picture above shows the angle of scattering in the CM frame. However experiments are done on ground - and not in the CM frame. So we should be answering the question: by what angle θ_lab does particle 1 scatter in the laboratory frame? Since velocities and in the lab frame are given as 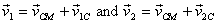, the relationship between these velocities can be shown as done in figure 6.

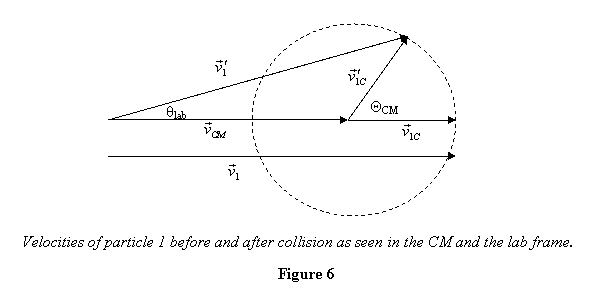
From figure 6, it is now very easy to see that

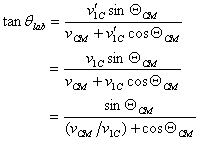
Similar relationships can also be derived for particle 2. Now if particle 2 was at rest when hit by particle 1, then

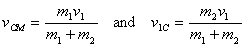
This gives

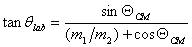
Let us now look at two cases: m₁ > m₂ and m₁ < m₂ . In the case of m₁ > m₂ , θ_lab cannot be greater than a particular angle θ_max. This can be either calculated by using the expression above or alternatively, graphically as we do. For m₁ > m₂ we also have v_CM >v_1C . Thus a picture showing the velocities in the laboratory and the CM frame looks like that in figure 7.

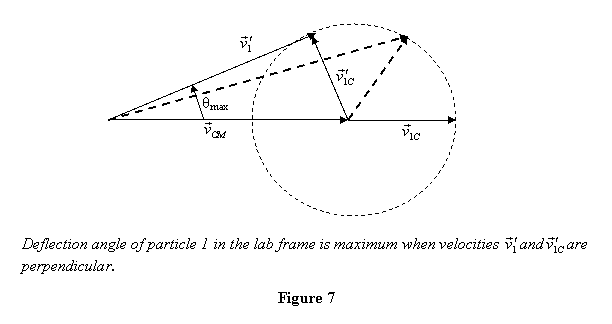
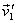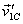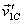It is clear from figure 7 that the deflection angle of particle 1, when hitting another particle of smaller mass, increases as Θ_CM increases from zero. It is maximum when the velocities and are perpendicular. If is rotates beyond this angle, deflection starts becoming smaller. Thus θ_max is given by the formula

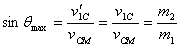
It is clear from the expression above that when a particle hits a lighter particle at rest, it is deflected by a small angle. This is reasonable as a light particle can hardy deflect a heavier particle. Thus the heavier particle keeps on moving forward even after the collision. On the other hand, there is no restriction on the scattering angle when a light particle hits a heavier particle at rest i.e. m₁ < m₂ . In this case v_CM < v_1C and therefore the graphical representation of different velocities is as shown in figure 8.

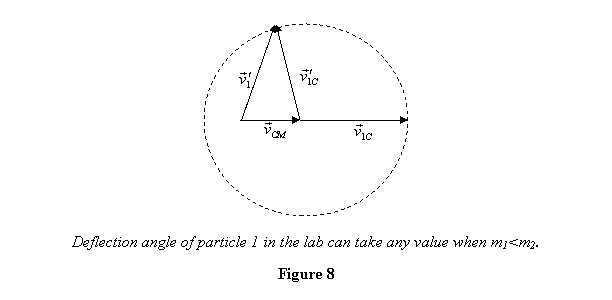
It is clear from the figure that as Θ_CM increases, so does θ_lab. In this situation, however, there is no restriction on the value that θ_lab can take as Θ_CM sweeps angles from 0 to 2π .

So far we have focused on elastic collisions only and could learn a great deal about them from conservation laws for momentum and energy. Such general conclusions are difficult to draw for inelastic collisions. As discussed in the beginning of this lecture, for inelastic collisions, we can definitely say that the maximum possible loss of energy is equal to the kinetic energy of particles in their CM frame. This would occur when the colliding particles get stuck together so that their kinetic energy after collision is zero in the CM frame. This concludes our lecture on collisions as analyzed using conservation laws.