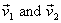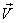As the first example, let us consider two particles of masses m₁ and m₂ moving with velocities , respectively, colliding, getting stuck together to make a particle of mass (m₁ +m₂ ) that moves with velocity . In the process energy ΔE is released. Then moment conservation tells us

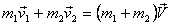
and balancing the energy gives

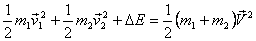
Notice that we have added to ΔE to the left-hand side so that the total final kinetic energy is the sum of the total initial kinetic energy and the energy added to the system. Substituting for 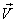from the momentum conservation equation in the energy equation, we get

which on simplification gives

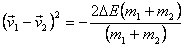
The left-hand side of the equation above is definitely positive. On the other hand, the right-hand side is negative if ΔE > 0 , i.e., the final kinetic energy is larger than the initial kinetic energy. So this reaction will not be possible if it is exothermic, i.e., some energy is generated and added to the initial kinetic energy. Thus two atoms colliding in free space will not combine to form a molecule (in which process the energy is usually released). However if energy is taken away from the system, i.e. ΔE < 0, then the reaction is possible. This is the information we have got purely on the basis of conservation laws. We now go on to discuss collisions as described with respect to the CM. We will see that this gives us a lot of insight into the collision problem.

As we had stated earlier, the conservation of momentum implies that the centre of mass moves with a constant velocity when there is no external force on the particles. Thus if we attach a frame to the CM, it will also move with constant velocity and will be an initial frame of reference. Let us call this the CM frame. Since it is an inertial frame, we can equally well describe a collision process is a CM frame. Observing a collision from the CM frame gives us the biggest advantage that the sum of the momenta (the total momentum) is always zero in this frame. In this lecture we will be focusing on two particle collisions as described from the CM frame. We will see that because of the total momentum being zero, description of a collision in this frame becomes simpler. In coming lectures we will see that CM provides a convenient origin for studying rotational motion also.

For now, let us look at the two particles collision. As stated above, in the CM frame the total momentum is always zero because in this frame the CM does not move. So that the velocities of two particles in the CM frame are always in the direction opposite to each other. Further the motion remains confined to a plane formed by the lines representing the initial and the final velocities directions (keep in mind that the velocities of the two particles at any instant are along the same line though opposite in direction). Thus in the CM frame a collision looks as shown in figure 2.

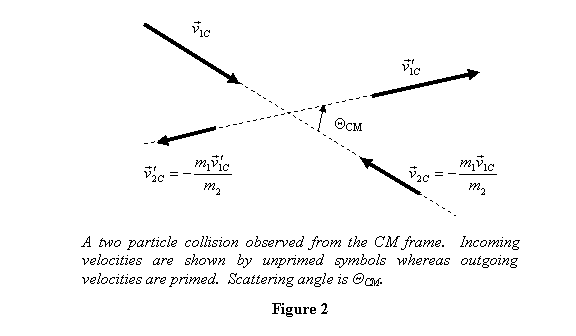
In figure 2 two particles with masses m₁ and m₂ and velocities 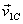and 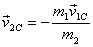are coming in for a collision; they collide and particle 1 goes out with velocity 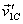and particle 2 with 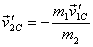. In the process particle 1 gets deflected by an angle Θ_CM. As stated earlier, even in 2d there are four unknowns: two components of 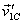and two of 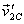to be obtained but only three equations- one for energy conservation and two for momentum conservation. So the problem cannot be solved fully by using conservation principle only. However, if the interaction is known, then Θ_CM and both the velocities after collision can in principle be calculated. Let us now see how much can we learn about the motion after collision applying only the conservation principles. We will be discussing both the elastic and inelastic collisions. Recall that if the kinetic energy remains unchanged in a collision, the collision is elastic; on the other hand, if the energy is lost the collision is inelastic.

Let us first focus on an elastic collision and analyze it in the CM frame. As pointed out earlier, the velocities of the two particles before and after collision are opposite to each other. Thus the relationship between the magnitudes v_1C , v_2C , v'_1C and v'_2C of the velocities is

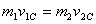
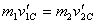
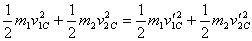
Substituting for 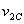and 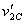from the first two equations in the last one we get

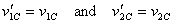
Thus the velocity vectors of both particles just rotate but do not change in magnitude as the partial move out after collision. You have learnt in previous classes that in an elastic collision the magnitude of the relative velocity of one particle with respect to the other remains unchanged during the collision. In one dimension it means that the speed of approach of two particles is the same as their speed of separation. Let us now see how it follows directly from the conservation principles.

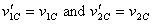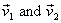As we have derived above, in an elastic collision. If the velocities of the two particles are , respectively, in the ground frame, then

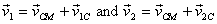
Similar relationships hold for the velocities after collision i.e.

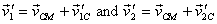
Using these relationships we find that

Similarly, we have

Thus we see that in an elastic collision

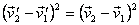
We have shown that the magnitude of relative velocity of one particle with respect to other remains the same in an elastic collision.

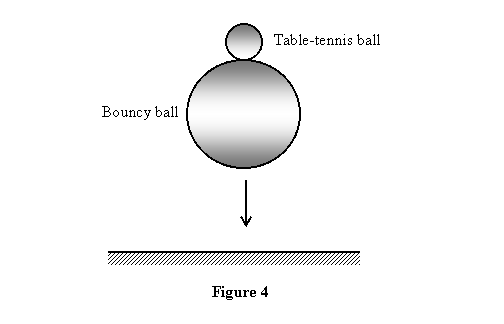
To see the dramatic effects of a nearly elastic collision, take a table-tennis ball (very small mass m), put it on a large bouncy ball of mass M (M >> m) , and drop them from a height (see figure 4) on a hard floor. You will see that the table-tennis ball bounces back really high after the balls hit the ground. Can you work how high will it go if the balls are dropped from a height h? Assume that no energy is lost.