Lecture 17
Collisions

In the previous two lectures, we have seen that when many particles are interacting, there are two conservation systems that are obeyed by them. One, if the net external force on the particles is zero, the total angular momentum of the system remains a constant. This is expressed mathematically as

Further we saw during the motion of a many particle system, one point - its centre of mass - moves as if its mass M is equal to the total mass 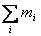of the system and the total force 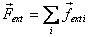is being applied on that mass. The CM co-ordinate is defines as

 

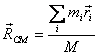
And it moves according to the equation

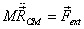
Thus if 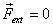then 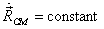. That means if the total external force on the system is zero, the CM moves with a constant velocity. This is another way of expressing the conservation of linear momentum.

The other conservation principle that we saw was that of total energy. Accordingly the total energy, which is the sum of their kinetic energy KE_i and potential energy PE_i , of a system of particles remains a constant

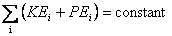
As an example of the power of these principles, in this lecture we apply these two principles to the problem of two particles of masses m₁ and m₂ colliding.

Before we discuss the problem of two particles colliding, we prove something very important and useful: Kinetic energy of a system of particles is equal to the sum of the kinetic energy of its centre of mass and kinetic energy of particles with respect to the centre of mass . 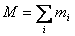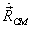By kinetic energy of the CM we mean its kinetic energy calculated as a point particle of the total mass moving with the velocity of the CM. To see this, substitute in the expression for the kinetic energy

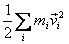
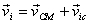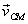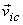, where is the velocity of the CM and is the velocity of i^th particle in the CM frame. This gives

Now 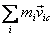is the momentum of the CM with respect to the CM and therefore proportional to the velocity of the CM with respect to the CM. But the velocity of the CM relative to the CM is zero implying that 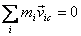. This immediately gives

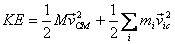
                                                         = KE of the CM + KE about the CM

This result, that the kinetic energy of a system of particles can be decomposed into KE of the CM and KE about the CM, is very important and useful. In a later lecture, we will see that the same is true for the angular momentum.

The division of kinetic energy as shown above is useful in learning how energies are shared when particles interact with each-other for short periods of time. As an example take explosion of a bomb. Since the CM will keep on moving the same way as it was before the explosion - because the forces generated are between the pieces of the bomb and therefore have no effect on the total momentum of the system - the explosion does not change the kinetic energy of the CM. Thus all the energy released in the explosion goes to the kinetic energy of the pieces of the bomb with respect to the CM. As another example, consider two particles colliding and getting stuck together. Since the CM keeps on moving with the same speed because of momentum conservation, the minimum kinetic energy that the masses stuck together have to have is that of the centre of mass. Thus the maximum possible energy loss in this case is the sum of their kinetic energy relative to their CM (also called the kinetic energy in the CM frame).

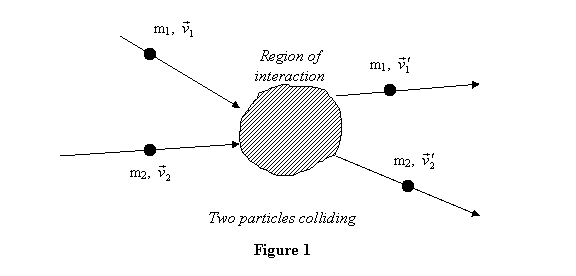
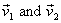We now get back to the problem of two particles colliding. We consider two particles of masses m₁ and m₂ coming in with velocities , respectively, interacting in a region, and then going out with velocities 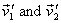(see figure 1). This is the simplest collision problem. If more particles are involved then the problem is going to be move complicated.

Since we assume particles interact only when they are close to each other, they are essentially free before and after the collision. Further, the interaction region is very small; thus even if the particles are in an external field, the potential energy remains essentially unchanged during the collision. Thus we can write

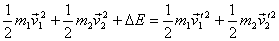
where we have added ΔE on the left-hand side to take into account any addition or loss of energy during the interaction of particles. For example if the particles generate some energy during interaction, ΔE > 0 . This will be the case when two particles release some chemical energy. On the other hand, ΔE < 0 when the particles lose energy during interaction. This is called an inelastic collision. ΔE = 0 is the case of elastic collision; here the total kinetic energy before and after the collision is the same. If particles interact over a large region, we can take the velocities to be in the asymptotic region, where the particles are far apart and therefore the equations above are applicable. The discussion so far has been in terms of balancing the energies involved during the interaction.

The other conservation principle is that of conservation of momentum. Usually during collision the impulse due to collision (internal force if two particles are considered as one system) is much larger than any external impulses. So we neglect it and conserve momentum. If the external impulse comparable to the internal impulse, it must be taken into account. This could be the case when the external force is very large or the particles interact for a long time. For the time being though, we will focus on cases where external impulse can be neglected. Thus

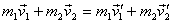
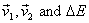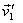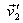The two equations are actually a set of four equations with momentum conservation giving three equations, one for each component. However, given , we have to solve for six quantities, three components for and three for . Thus to solve the problem completely, we need more information, for example the scattering angles. In two dimensions also, the conservation equations alone are not enough to solve the problem of finding velocities after the collision. This is because now there will be four unknowns - two components for velocity of each particle - but only three equation, one from the energy balance and two from momentum conservation. Only in one dimension, we can solve the collision problem completely because there are two equations and two unknowns. Nonetheless, we can get a lot of information about the motion from these two conservation laws as we now discuss.