Learning about force and motion
from the potential energy
We learnt above about how the force leads to the concept
of potential energy. However, it is the potential energy
that is easier to specify than the force. The reason
is very simple: force is a vector quantity and as such
in specifying it we have to give its three components
as a function of position. On the other hand, potential
energy is a scalar quantity and is easier to write as
a function of position. For the same reason, many a times
it is easier to calculate the potential energy than to
calculate the force, as we will see in an example below.
Thus generally we give the potential energy of a particle
to tell about the force field in which the particle is
moving. In this section we discuss what can we learn
about the motion of a particle by looking at its potential
energy.
First we discuss how do we get the force from the potential
energy. Let us first look at one-dimensional case. Employing
the definition of potential energy, we find that for
a small displacement Δx
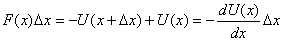
which means that the force is given by the formula
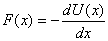
This is the key formula relating the force to the potential
energy. On the basis of this formula, we can infer a
lot about the nature of motion by looking at the potential
energy curve. First if 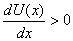 ,
then the force is towards the negative x-direction and
if ,
then the force is towards the negative x-direction and
if 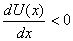 ,
the force is towards the positive x-direction. Thus the
force is in the direction of decreasing U(x).
What if ,
the force is towards the positive x-direction. Thus the
force is in the direction of decreasing U(x).
What if 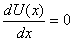 ?
In that case the particle in either on a maximum or a
minimum of the potential and there is no force on the
particle. The particle is therefore in equilibrium. The
equilibrium will be stable one, that is the particle
will come back to the equilibrium point when displaced
slightly from that point, if it is at the potential energy
minimum or equivalently where ?
In that case the particle in either on a maximum or a
minimum of the potential and there is no force on the
particle. The particle is therefore in equilibrium. The
equilibrium will be stable one, that is the particle
will come back to the equilibrium point when displaced
slightly from that point, if it is at the potential energy
minimum or equivalently where 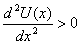 .
On the other hand at the maximum of the potential energy,
the particle will rush away from that point if it is
disturbed. Thus at the potential energy maximum, where .
On the other hand at the maximum of the potential energy,
the particle will rush away from that point if it is
disturbed. Thus at the potential energy maximum, where 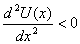 ,
the equilibrium is unstable. We see that a particle tends
to move towards its potential energy minimum and move
away from its potential energy maximum. All these concepts
can be shown nicely with a bead moving on a smooth frictionless
wire bent in the shape of a curve with many maxima and
minima and held in the vertical plane (see the figure
below). The potential energy of the bead is then proportional
to the height of the curve and as such the wire itself
represents the potential energy curve in the figure below. ,
the equilibrium is unstable. We see that a particle tends
to move towards its potential energy minimum and move
away from its potential energy maximum. All these concepts
can be shown nicely with a bead moving on a smooth frictionless
wire bent in the shape of a curve with many maxima and
minima and held in the vertical plane (see the figure
below). The potential energy of the bead is then proportional
to the height of the curve and as such the wire itself
represents the potential energy curve in the figure below.
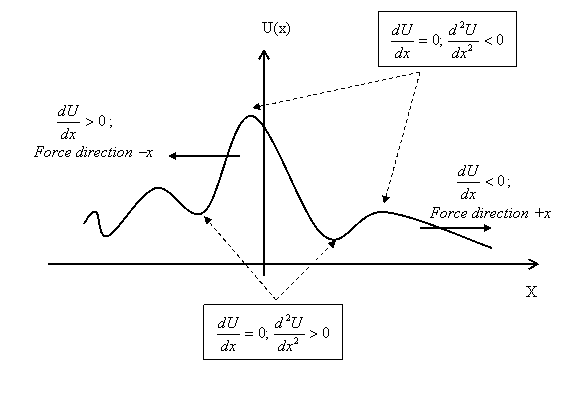
Now with a bead sliding over the wire, you can easily
check that all the points made above about the relationship
between the force on the bead and the mathematical properties
of the potential energy curve are correct. Further the
minima and maxima of the curve are clearly observed to
be stable and unstable equilibrium points, respectively.
In three dimensions the equivalent of the derivative is
the gradient operator. Thus the force 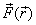 in
two or three dimensions is given as in
two or three dimensions is given as
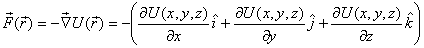
Thus the force is in the direction opposite to that of
increasing U. Further, it vanishes wherever the gradient
of the potential energy is zero. Individual components
of the force are given as
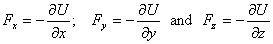
A word of caution is needed here. 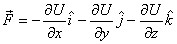 does
not mean that if we transform to some other co-ordinates
system (say spherical) then does
not mean that if we transform to some other co-ordinates
system (say spherical) then
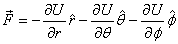
will be correct. This is not even dimensionally correct.
To get the correct answer, one must properly transform
from Cartesian to polar co-ordinates. The result then
is
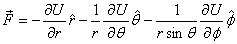
Thus in spherical polar coordinate system, the force components
are given as
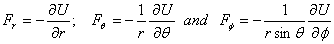
Similarly in cylindrical coordinate system the force is
related to the potential energy as
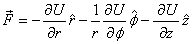
With the individual force components
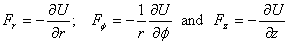
Having given you the prescription for obtaining force
from the potential energy let us now apply it to find
the field of an electric dipole using its scalar potential.
Example: As an application of finding
force from the potential, let us calculate the electric
field due to a dipole.
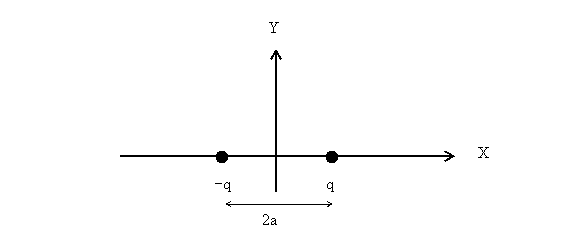
Let the dipole be situated at the origin along the x-axis.
Let the charges -q and +q be separated
by distance 2a (see figure below) so that the
dipole moment is 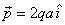 .
Then potential and field at any point can be calculated
by adding the field due to the two charges. Adding the
field in this case becomes a bit difficult because we
have to obtain three components of the field for each
charge and add them. On the other hand, finding the potential
is relatively easy because it is a scalar quantity and
we obtain it by adding the potential due to two charges.
Then the gradient gives the field. In the calculation
we assume that a → 0 and q is correspondingly
very large so that their product is finite. We will be
using this by keeping term only linear in a and
neglecting higher orders. .
Then potential and field at any point can be calculated
by adding the field due to the two charges. Adding the
field in this case becomes a bit difficult because we
have to obtain three components of the field for each
charge and add them. On the other hand, finding the potential
is relatively easy because it is a scalar quantity and
we obtain it by adding the potential due to two charges.
Then the gradient gives the field. In the calculation
we assume that a → 0 and q is correspondingly
very large so that their product is finite. We will be
using this by keeping term only linear in a and
neglecting higher orders.
The potential (potential energy per unit charge) due the
two charges is given as
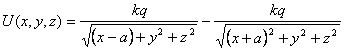
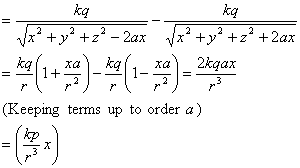
Now taking the gradient we get the three components of
the force, which are
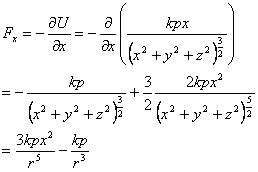
Similarly

Combining these results together we get for the field
of the dipole
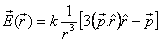
I would like you to get the same result by adding the
fields of the charges together and compare the answers.
In these lectures, we have learnt: the work-energy theorem,
definition of potential and its relationship with the
force field, concept of conservative forces and the principle
of conservation of energy. I leave these lectures by
giving you a few exercises.
Exercise 1: Consider one-dimensional
motion in a potential U(x). Show that if a particle of
mass m is displaced slightly from its equilibrium
position at a potential energy minimum at x0 ,
it will perform simple harmonic oscillations. Find the
corresponding frequency.
Exercise 2: Consider two different inertial
frames moving with respect to one another with a constant
velocity. Starting from the work-energy theorem in one
frame, prove that it is true in the other frame also. |