Example: Take the force field given by 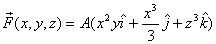and consider a particle moving from A to be along the semicircular path ACB (see figure below). Calculate the difference in its kinetic energy at B and at A.

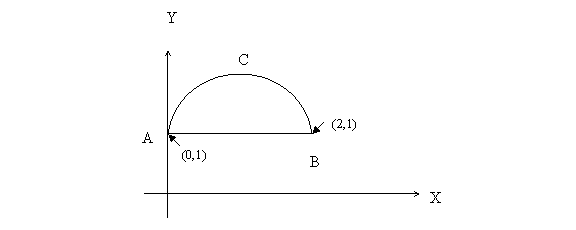
To calculate the change in the kinetic energy of the particle as it moves from A to B, we should calculate the work done by the force in when the particle travels along the semicircle. For this we should calculate

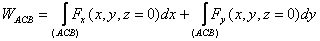
with y and dy calculated from the equation of the circle 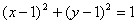. You should try it and see for yourself that the integrals become really lengthy. On the other hand, if the force is conservative, we can calculate the work done in particle moving along the diameter. The latter calculation is much easier. Let us therefore first calculate the curl of the force. It is

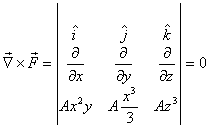
Thus the work done between any two points is path-independent. We therefore calculate the work along the diameter AB. It is

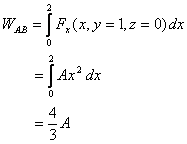
Since the work done is independent of the path, it is going to be the same for the semicircular path ACB also.

After defining the potential energy and getting the principle of conservation energy, we now look a little more at the relationship between the potential energy and the force it gives rise to. As a consequence we also discuss what can we learn about the motion of a particle by looking at its potential energy curve.