Work
and energy in three dimensions
As we already know, work is defined as the scalar product
of the force and displacement vector. Thus if a particle
moves under the influence of a force field 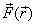 from
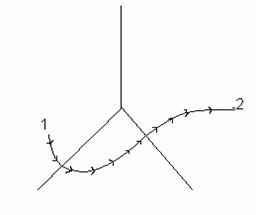
point 1 to point 2 along the path shown below, the total
work is calculated as the sum of partial work done when
the particle moves a vanishingly small distance from
point 1 to point 2 along the path shown below, the total
work is calculated as the sum of partial work done when
the particle moves a vanishingly small distance 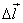 along
the arrows shown below in the figure. along
the arrows shown below in the figure.
Thus the total work done in gives as
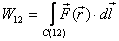
where C(12) indicates that the particle is moving
along the curve C from point 1 to 2 .
Writing the dot product explicitly, we get
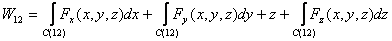
where Fi (i = x,y,z) indicates the
ith component of the force and x, y and z are
varied along the curve. Let us do an example of calculating
the work in this manner in two-dimensions.
Example: Consider two force fields (a) 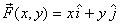 ,
and (b) ,
and (b) 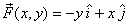 in
the x-y plane. Calculate the work done by these forces
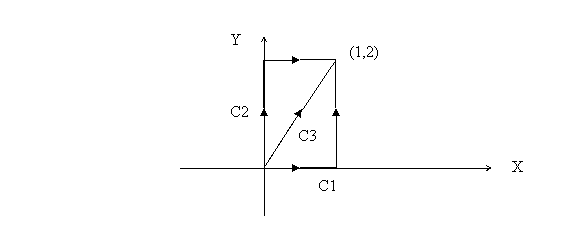
when a particle moves from the origin to (1,2) along
the three paths C1, C2 and C3 shown in the figure below.
On C1 the particle goes along the x-axis first and then
moves parallel to the y-axis; on C2 it travels along
the y-axis first and then parallel to the x-axis and
on C3 it moves along the diagonal. in
the x-y plane. Calculate the work done by these forces
when a particle moves from the origin to (1,2) along
the three paths C1, C2 and C3 shown in the figure below.
On C1 the particle goes along the x-axis first and then
moves parallel to the y-axis; on C2 it travels along
the y-axis first and then parallel to the x-axis and
on C3 it moves along the diagonal.
The work done is given by the formula
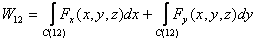
Along C1 y = 0 , dy = 0 while moving
along the x-axis whereas x = 1 and dx =
0 when
the particle travels parallel to the y-axis. Thus the
work done along C1 is
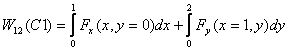
Similarly work done along C2 is given as
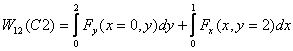
For path C3, we have y = 2x so that dy =
2dx .
Therefore we substitute y = 2x in the functions
giving the force and replace dy by 2dx .
As a result, the final integration is over x only
with x varying from 0 to 1 .
Thus the work done is
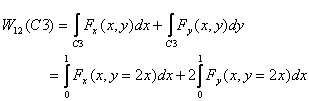
We are now ready to work out the work done by force in
(a) and (b) (I would like you to plot these force fields
and leave it as an exercise for you). For the force in
(a) we get
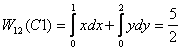 ; ;
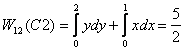 ; ;
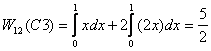
For force (b) on the other hand we get
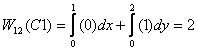
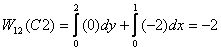
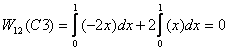
Thus we see that whereas the force in (a) gives the work
to be the same for all three paths, that in (b) gives
different work along the three paths. Thus the first
force field may be conservative but the second one is
definitely not.
Now let us derive the work-energy theorem in three dimensions.
Start from the equation of motion 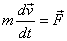 and
take the dot product of both sides with the velocity and
take the dot product of both sides with the velocity 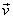 to
get to
get
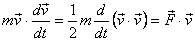
Now integrate both sides with respect to time and use 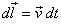 ,
where ,
where 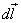 is
the small distance traveled by the particle in time interval dt ,
to get is
the small distance traveled by the particle in time interval dt ,
to get
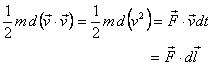
On integration this leads to
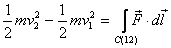
This equation tells us that when a force makes a particle
move along path C from point 1 to 2, the work done by
the force equals the change in its kinetic energy. This
is the work-energy theorem in three-dimensions. It is
exactly the same as in one dimension except that the
work done is calculated by moving along a three-dimensional
path.
Potential energy: As is the case in
one dimensional motion, potential energy in general can
be defined only if the work done is path independent.
In that case, the work done depends only on the end points
of the path of travel and can be written as the difference
on a quantity that is a function of the position vector
only. Thus
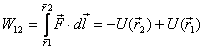
where 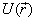 is
defined as the potential energy. Notice that this time
I have not written any specific path but just the end
points with the integral sign because the work is supposed
to be path-independent. From the definition above, it
is also evident that here too the difference in the potential
energy is
defined as the potential energy. Notice that this time
I have not written any specific path but just the end
points with the integral sign because the work is supposed
to be path-independent. From the definition above, it
is also evident that here too the difference in the potential
energy 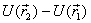 between
point 1 and point 2 is the work
done by us in moving a particle slowly, maintaining
its equilibrium, from point 1 to point 2.
Now following the exactly same steps that we did for
the one dimensional case, we show that between
point 1 and point 2 is the work
done by us in moving a particle slowly, maintaining
its equilibrium, from point 1 to point 2.
Now following the exactly same steps that we did for
the one dimensional case, we show that
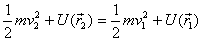
Thus when the potential energy can be defined, the total
mechanical energy of a particle is conserved .
I remind you that the total mechanical energy is the
sum of the kinetic and the potential energies. In such
cases the force is said to be conservative.
By now you may be wondering how can we find out whether
a force is conservative or not. Do we have to calculate
the work done along all possible paths before we can
say that the force is conservative and therefore the
principle of conservation of energy holds good. That
certainly would be impossible to do. However, there is
a much simpler test to check whether a force field is
conservative or not. I am going to tell you about it
without giving the proof. To find out about the conservative
nature of a force 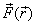 ,
we calculate its curl ,
we calculate its curl 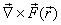 defined
as defined
as
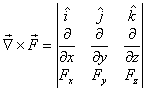
Now if the curl of a force field vanishes everywhere,
it is a conservative force field. On the other hand if
the curl of a force field is nonzero, it is not conservative.
Let us now apply this test to the two force fields for
which we calculated the work done along different paths.
For the force field 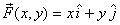 ,
the curl is zero everywhere. Hence it is conservative
and, as we saw with three paths, the work done in this
field is indeed path independent. On the other hand,
for ,
the curl is zero everywhere. Hence it is conservative
and, as we saw with three paths, the work done in this
field is indeed path independent. On the other hand,
for 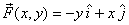 ,
the curl comes out to be ,
the curl comes out to be 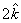 and
therefore the force is not conservative. This was seen
above where the work done along the three paths were
all different. We now solve an example where knowing
the conservative nature beforehand helps us avoid an
unnecessary calculation. and
therefore the force is not conservative. This was seen
above where the work done along the three paths were
all different. We now solve an example where knowing
the conservative nature beforehand helps us avoid an
unnecessary calculation.
|