Conservation of energy: Having defined potential energy we now combine it with the work energy theorem to come up with another very important conservation principle: that of conservation of energy . This is obtained as follows. By the work energy theorem

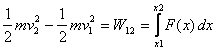
and by definition of the potential energy

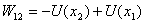
Combining the two equations we get

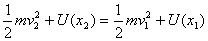
This equation means that if a particle moves in a force field where the work done by the force does not depend on the path taken, the sum of its kinetic and potential energy remains unchanged from one point to another. The sum of the kinetic and potential energy is known as the total mechanical energy. Thus in a force field for which the potential can be defined, total mechanical energy is conserved. Such force fields, where the total mechanical energy is conserved, are therefore known as conservative force fields. Thus whereas the example above is a conservative force field, frictional force is not. Question: If the potential energy is explicitly time-dependent, is the total energy conserved?

We now move on to generalize and discuss these concepts in three-dimensions.