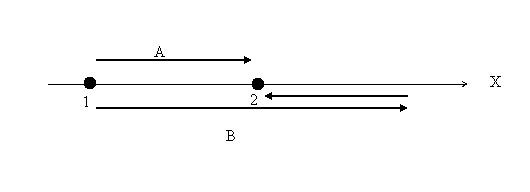
Potential energy: Let us now define another related energy known as the potential energy . This defined for a force field that may exist in the space, for example the gravitational field or the electric field. Before doing that we first note that even in one dimension, there are many different ways in which one can go from point 1 to point 2 . Two such paths are shown in the figure below.

On path A the particle goes directly from point 1 to 2 , whereas on path B it goes beyond point 2 and then comes back. The question we now ask is if the work done is always the same in going from point 1 to point 2. This is not always true. For example if there is friction, the work done against friction while moving on path B will be more that on path A. If for a force the work done depends on the path, potential energy cannot be defined for such forces. On the other hand, if the work W₁₂ done by a force in going from 1 to 2 is independent of the path, it can be expressed as the difference of a quantity that depends only on the positions x₁ and x₂ of points 1 and 2
(Question: If the work done is independent of path, what will be the work done by the force field when a particle comes back to its initial position? ). We write this as

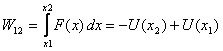
and call the quantity U(x) the potential energy of the particle. We now interpret this quantity. Assume that a particle is in a force field F(x) . We now apply a force on the particle to keep it in equilibrium and move it very-very slowly from point 1 to 2. Obviously the force applied by us is - F(x) and the work done by us in taking the particle from 1 to 2, while maintaining its equilibrium, is

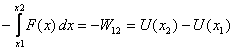
Thus for a given force field, the potential energy difference U(x₂ ) - U(x₁ ) between two points is the work done by us in moving a particle, keeping it in equilibrium, from 1 to 2 . Note that it is the work done by us - and not by the force field - that gives the difference in the potential energy. By definition, the work done by the force field is negative of the difference in the potential energy. Further, it is the difference in the potential energy that is a physically meaningful quantity. Thus is we want to define the potential energy U(x) as a function of x , we must choose a reference point where we take the potential energy to be zero. For example in defining the gravitational potential energy near the earth's surface, we take the ground level to be the reference point and define the potential energy of a mass m at height h as mgh . We could equally well take a point at height h₀ to be the reference point; in that case the potential energy for the same mass at height h would be mg(h - h₀ ) . Let us now solve another example.

Example: A particle is restricted to move along the x-axis and is acted upon by a force 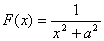. Find its potential energy.

We first note that the force is always acting towards the positive x-direction. Thus when we move the particle, we will have to do positive work when taking it towards the negative direction. Thus we expect the potential energy to increase as x becomes more and more negative. By definition

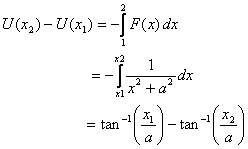
Now we choose our reference point. If we choose U(x₁ = ∞) = 0 , the potential energy is given as

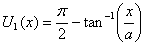
On the other hand if we choose U(x₁ = 0) = 0 , we get

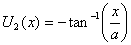
The two energies are shifted with respect to one another by a constant so that the difference in the potential energy between two points is the same for both the forms, as pointed out earlier. The potential energy is lowest for x = ∞ and increases as we move towards left and becomes largest for x = - ∞ . This is precisely what we had anticipated above on the basis of the meaning of potential energy.