The equation of motion in one-dimension (taking the variable to be x, and the force to be F ) is

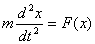
Let us again eliminate time from the left-hand using the technique used above

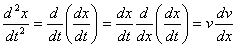
to get

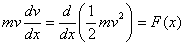
On integration this equation gives

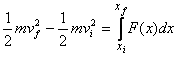
where x_i and x_f refer to the initial and final positions, and v_i and v_f to the initial and final velocities, respectively. We now interpret this result. We define the kinetic energy of a particle of mass m and velocity v to be

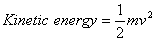
and the work done in moving from one position to the other as the integral given above

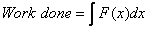
With these definitions the equation derived above tells us that work done on a particle changes its kinetic energy by an equal amount; this known as the work-energy theorem .

You may ask: how do we know this equation to be true and consistent with our observations? This is the question that was asked in the early eighteenth century when it was not clear how to define energy, whether as mv or as mv² ? The problem with the definition as mv is that if two particles moving in the opposite directions have their energies canceling each other and if they collide, they stop and all the energy is lost . On the other hand, defining it proportional to v² makes their energies add up and noting is lost during collision; the energy just changes form but is conserved. Experimental evidence for the latter was found by dropping weights into soft clay floors. It was found that by increasing the speed of the weights by a factor of two made them sink in a distance roughly four times more; increase in the speed by a factor of three made it nine times more. That was the evidence in favor of kinetic energy being proportional to v² .