Lecture 15 & 16
Work and Energy

You have been studying in your school that we do work when we apply force on a body and move it. Thus performing work involves both the application of a force as well as displacement of the body. We will now see how this definition comes about naturally when we eliminate time from the equation of motion.

The question that immediately comes to mind is why should we eliminate time from the equation of motion. This is because when we follow the motion of a particle, we are usually interested in velocity as a function of position. Secondly, if we write the equation of motion in terms of time derivatives, it may make the equation difficult to solve. In such cases eliminating time from the equation of motion helps in solving the equation. Let us see this through an example.

Example: Consider the motion of a particle in a gravitational field of mass M . Gravitational force on a mass m is in the radial direction and is given as

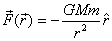
Since the force in the radial direction, it is better to write the equation of motion in spherical polar coordinates. For simplicity we consider the motion only along the radial direction so that the equation of motion is written as

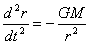
As you can see, integrating this equation to get r(t) as a function of time is very difficult.

On the other hand, let us eliminate time from the equation by using chain rule of differentiation to get

,

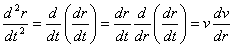where 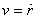  is the velocity in the radial direction. This changes the equation of motion to

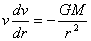
This equation is very easy to integrate and gives 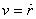as a function of r, which can hopefully be further integrated to get r as a function of time. Now we go back to what I had said earlier that the definition of work and energy arises naturally when we eliminate time from the equation of motion. Let us do that first for one dimensional case and analyze the problem in detail.