As
an example let us calculate the pressure of a gas filled
in a container. Let the mass of each molecule be m and
let their average speed be v . The number density
of the molecules in the gas is taken to be n .
Now consider a surface of the container perpendicular
to the x-axis. (see figure 8).

Each molecule, when reflected from the wall imparts
a momentum equal to 2mvx to
the wall. The average number of molecules hitting
are A of
the wall per unit time will be half of those
contained in a cylinder of base area A and
height vx (the
other half will be moving in the other direction).
This comes out to be 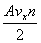 .
Thus from the formula derived above the force
on the wall applied by these molecules is .
Thus from the formula derived above the force
on the wall applied by these molecules is
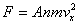
which gives the pressure
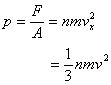
This is a result you are already familiar with kinetic
theory of gases. But now you know how it comes out. Having
done this problem we now deal with another very interesting
application of the momentum-force relationship, known
as the variable mass problem.
So far we have been dealing with particles of fixed
masses. Let us now apply the equation 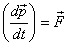 to
a problem when the mass of the system under consideration
varies with time. The most famous example of this
is the rocket propulsion. to
a problem when the mass of the system under consideration
varies with time. The most famous example of this
is the rocket propulsion.
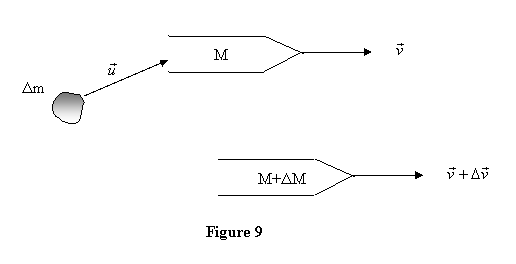
Let a rocket with mass M at time t be
moving with velocity 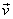 .
A small mass Δm with velocity .
A small mass Δm with velocity 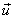 comes
and gets stuck with it so that the rocket now has
mass M + Δm and moves with
a velocity comes
and gets stuck with it so that the rocket now has
mass M + Δm and moves with
a velocity 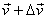 (see
figure 9 below) after a time interval of Δt.
We want to find at what rate does the velocity of
the rocket increase? We point out that the word
rocket has been used here to represent any system
with variable mass . (see
figure 9 below) after a time interval of Δt.
We want to find at what rate does the velocity of
the rocket increase? We point out that the word
rocket has been used here to represent any system
with variable mass .
Let us write the momentum change in time interval Δt and
equate this to the total external force on the system
(that is the sum of external forces acting on M and Δm)
times Δt.
That gives
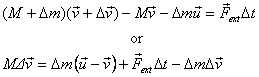
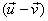 is
nothing but the relative velocity is
nothing but the relative velocity 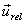 of
the mass Δm with respect to the rocket. of
the mass Δm with respect to the rocket.
Dividing both sides of the equation above by Δt then
leads to
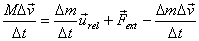
We now let Δt → 0 . In this limit 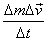 also
goes to zero for continuously varying mass. Further, also
goes to zero for continuously varying mass. Further, 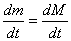 ,
the rate of change of the mass of the rocket.
Thus the equation for the velocity of a rocket
is ,
the rate of change of the mass of the rocket.
Thus the equation for the velocity of a rocket
is
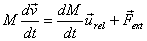
Note that both the mass and velocity are now functions
of time. For a rocket 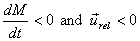 so
that so
that 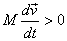 .
It is this term that provides the thrust to the
rocket. As pointed out above, although
this equation has been derived keeping rocket
in mind, it is true for any system with variable
mass . .
It is this term that provides the thrust to the
rocket. As pointed out above, although
this equation has been derived keeping rocket
in mind, it is true for any system with variable
mass .
Example: We now solve a simple problem
involving the rocket equation. A rocket is fired vertically
up in a gravitational field. What is its final velocity
assuming that the rate of exhaust and its relative velocity
remain unchanged during the lift off?
The motion of rocket is one-dimensional. We take the
vertically up direction to be positive. Then we have 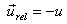 where u is
a positive number. Therefore the rocket equation
takes the form where u is
a positive number. Therefore the rocket equation
takes the form
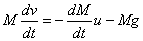
which gives
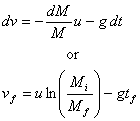
Here we have taken the initial time and initial velocity
both to be zero. Even after the fuel has all been burnt,
we see if we observe the rocket time t after
being fired, its velocity will be given by the formula
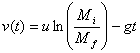
assuming g to be a constant.
Finally, although the momentum-force equation can provide
answers for the velocities, I would like to urge you
to always think about how the internal forces that generate
momenta in opposite directions are generated. That helps
in understanding the underlying physics better. For example
in the rocket problems, we say that 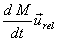 provides
the thrust to make the rocket move forward. But think
about what generates this force? The answer is as follows.
In a closed container, gas pressure applies force in
all directions and these forces cancel each other. But
when a hole is made from where the gas can escape, the
force in the opposite direction is unbalanced; and that
is what makes the rocket move. If you understand this,
you should e able to answer the following question. If
we take a closed box with vacuum inside and punch a hole
in it. Which way will it move? provides
the thrust to make the rocket move forward. But think
about what generates this force? The answer is as follows.
In a closed container, gas pressure applies force in
all directions and these forces cancel each other. But
when a hole is made from where the gas can escape, the
force in the opposite direction is unbalanced; and that
is what makes the rocket move. If you understand this,
you should e able to answer the following question. If
we take a closed box with vacuum inside and punch a hole
in it. Which way will it move?
We conclude this lecture by summarizing what we have learnt.
We studied the conservation of momentum and a related
concept of the centre of mass. Using momentum, we then
calculated the force on a surface being hit by a stream
of particles, or jet of water. Finally we learnt about
the variable mass problem and applied it to a rocket
taking off. In the coming lecture we will use the conservation
of momentum principle along with the conservation of
energy and see how this combination becomes a powerful
tool in solving mechanics problems.
|