I now discuss a little about calculation of the centre
of mass of a mass distribution. Calculation of the centre
of mass is similar to calculating the centroid of an
area (lecture 7), except that the area is now replaced
by mass. For finite masses at given positions, the definition
of centre of mass given above is used directly. For a
mass distribution in three-dimensions, we calculate all
three components of the poison of the centre of mass.
These are given as
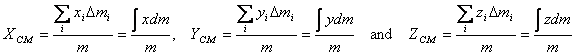
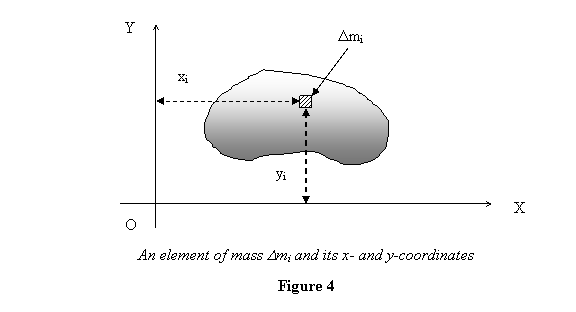
where dm is a small mass element at the
position (x,y,z) in the mass distribution
(see figure 4 below).
We are now going to change the topic a bit and ask
how we describe a system where a large force acts
for very short durations. A cricket bat striking
a ball, a hammer hitting a nail, a person jumping
on a floor and coming to sudden stop and a carom
striker hitting a coin, or collisions in general,
are examples of such forces in operation. In these
cases it is not meaningful to talk about the force
as a function of time because the time span over
which the force acts is very-very short. Further,
the force varies a great deal over this short
time-interval, as I show in an example below. It
is therefore better to describe the overall impact
of the force in terms of the momentum change it causes
to the system. This is given by the integral of the
force over the time that it operates. Thus 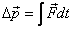 describes
the effect of the force on the system. The integral describes
the effect of the force on the system. The integral 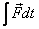 is
known as the impulse and denoted by the symbol J.
Obviously the momentum change of a system equals
the impulse given to it. We now discuss these
ideas with the help of an example, that of a
ball hitting a wall or any other hard surface. is
known as the impulse and denoted by the symbol J.
Obviously the momentum change of a system equals
the impulse given to it. We now discuss these
ideas with the help of an example, that of a
ball hitting a wall or any other hard surface.
Let us ask what happens when a ball hits a wall or we
jump on the floor. If the ball hitting the wall reflects
back, that means that the wall has applied a force on
the ball so that
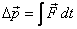
If the time of contact between the ball and the wall
is 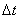 seconds
then the average force is seconds
then the average force is
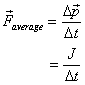
But the real force varies greatly from the average force.
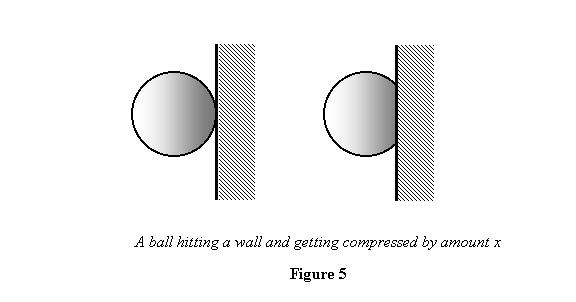
We show that now. Take the model of the ball as following
Hooke's law so that if it is compressed by x by
the wall, it applies a force kx on the wall
and consequently experiences an equal force in the opposite
direction (see figure 5 below).
Since the force on the ball follows Hooke's law, the
ball performs a simple harmonic motion, its compression
is given by 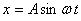 ,
where A is the maximum compression and ,
where A is the maximum compression and 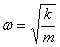 .
From time t = 0 , when the ball comes
in and touches the wall, it takes .
From time t = 0 , when the ball comes
in and touches the wall, it takes 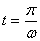 time
(half a cycle) before leaving the wall. The force
during this time is given as time
(half a cycle) before leaving the wall. The force
during this time is given as
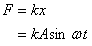
Since for a hard ball k is very large, 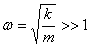 .
So by the time the ball comes back, the force
varies with time as shown in the figure 6 below.
Here the
maximum force Fmax is
given by kA and .
So by the time the ball comes back, the force
varies with time as shown in the figure 6 below.
Here the
maximum force Fmax is
given by kA and 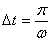 .
In the figure we show both Fmax and Faverage .
The latter is calculated as .
In the figure we show both Fmax and Faverage .
The latter is calculated as
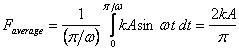
or
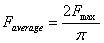
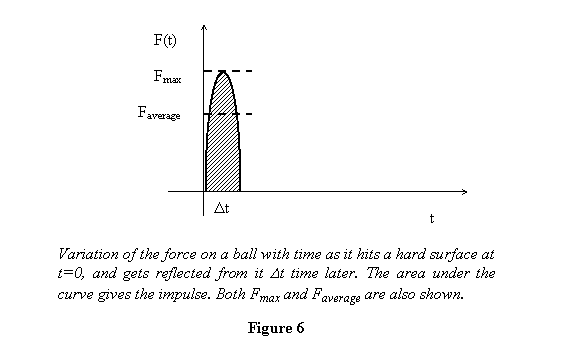
So you see that over this short period force varies a
great deal and is hardly ever near the average force
that we calculated. The discussion above has been in
terms of a model of the force; the exact force will be
different this model and so the variation could be even
larger than that shown. It is in such situations, when
a strong force is applied over a very short time period,
that it is much more meaningful to talk of the total
momentum change of a particle than the force 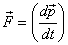 .
Further, in such cases, we generally observe
only the initial & final momentum and are
hardly concerned about the finer details. It
is this change .
Further, in such cases, we generally observe
only the initial & final momentum and are
hardly concerned about the finer details. It
is this change
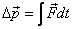
In the momentum that is known as the impulse. So in
the ball rebounding from a hard surface with the
same speed as it comes in with, the impulse is 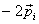 ,
where ,
where 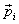 is
the initial momentum of the ball. So instead
of talking of the force applied by the ball on
the surface, we say that the ball has imparted
momentum to the surface it hit. The amount of
momentum transferred is equal to the impulse.
This has interesting application in calculating
the force on a surface when there are many-many
particles continuously hitting a surface, for
example molecules in a vessel hitting its walls
from inside. is
the initial momentum of the ball. So instead
of talking of the force applied by the ball on
the surface, we say that the ball has imparted
momentum to the surface it hit. The amount of
momentum transferred is equal to the impulse.
This has interesting application in calculating
the force on a surface when there are many-many
particles continuously hitting a surface, for
example molecules in a vessel hitting its walls
from inside.
We show two situations in figure 7 below. The upper
figure shows the variation of force on a wall when
particles hit a surface at some time interval. The
lower one, on the other hand, shows the situation
when particles hit continuously. In the first case
the force on the surface due to the particles hitting
it varies pretty much like the force due to each
particle itself. In the second case, however, the
force at any instant is given as the sum of the forces
applied by each particle at that time. This gives
an almost constant force Fmany as
shown in the figure. The value of this force is calculated
as follows. Let each particle hitting the surface
impart an impulse J to it. If on an average
there are n particles per second hitting
the surface, then in time Δt the momentum transferred
to the surface will be (nΔt)J.
The force Fmany will
then be given as
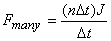
Since 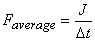 ,
the force above can also be written as ,
the force above can also be written as
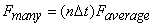
Thus when a stream of particles hits a surface, the force
applied by them to the surface equals the
number of particles striking in time Δt
times the average force applied by each one of
them, a result that you could have anticipated. This
is precisely what happens when a jet of water or flowing
mass hits another object.
|