Let us take an example.

Example 1: Suppose a bomb dropping vertically down explodes in mid air and breaks into three parts. Let the mass of the bomb be m and those of three pieces 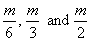, respectively. If the heaviest piece falls 10m to the east and the lightest piece 12m south of where the unexploded bomb would have dropped, where does the third piece fall?

Since 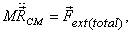the CM keeps on moving - even after the bomb breaks - vertically down as if it were a point mass of mass M falling under gravity. Thus the CM hits the ground where the unexploded bomb would have fallen. Let us take this point to be the origin with east side being the positive x-axis and the north side the positive y-axis. Then 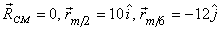after the bomb pieces having moved for equal times. By definition of the centre of mass we have

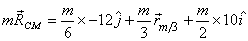
With 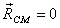, this gives

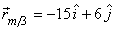
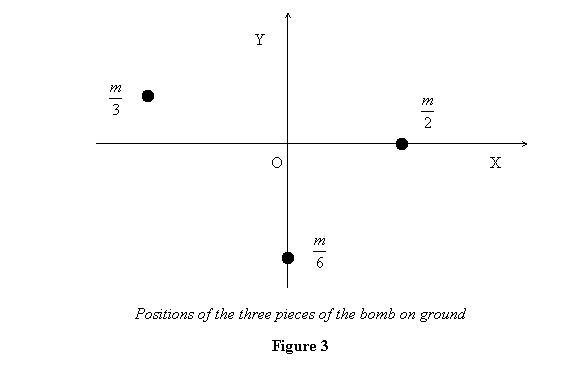
Relative positions of the three pieces are shown in figure 3 below, with the centre of mass at the origin.

You see that having the knowledge about the position of the other two pieces, we have got the position of the third piece without the knowing anything about the forces generated during the explosion and therefore without solving any equation of motion. That is the power of the momentum conservation principle. I will leave it for you to think which component of momentum is conserved in this case. Would that component be conserved if drag force were included?

Other familiar examples of momentum conservation are a gun recoiling when fired, two persons on roller seats pushing each other and consequently moving away from each other. Look around and you will find many such examples of momentum conservation.