Lecture 14
Momentum

So far we have dealt with motion of single particles. Now we are going to make the situation slightly more difficult by letting two or more particles apply forces on one another either by coming in contact or from a distance, and see how we can describe their motion. In such a situation the motion become much more interesting. Let us take an example of only two particles interacting through a spring connected to them, as shown below.

During their motion any of the following could take place: the distance between them may change,

or their orientation may change,

or a combination of both these may occur. Now we wish to develop methods of dealing with such situations. We do this gradually by taking one step at a time. In this regard, we start by introducing the quantity momentum that plays a very important role in describing motion when more than one point particle are involved in the motion.

To understand the importance of momentum, let us do the following experiment. Take a cart moving on a frictionless horizontal plane and start putting mass into it; it may be dropped vertically in it (see figure 1 below).

You will see that the cart starts slowing down. If we wish to keep it moving with the same velocity, we find that we have to apply a force on it

Compare this with the standard form of Newton's II^nd law where we put

So we see that whether the mass is changed and the velocity kept constant, or the velocity is changed and the mass is kept constant, we have to apply a force to a body. Thus in general

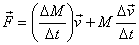
(We have ignored the second-order term   right now assuming that both the mass and the velocity are varying continuously). Therefore

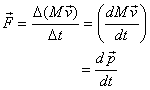
and this defines for us a quality called the momentum denoted above by 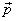. By definition

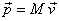
The force applied on a body or a system of particles is then the rate of change of their total momentum, i.e.

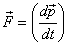
where 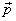now refers to the momentum of the system made up of a collection of particles. In the example taken above, we have to apply a force to keep the cart moving with a constant velocity because as the mass falls in the cart and starts moving with same velocity as the cart, the total momentum of the system - the cart and the mass in it - increases. In writing the definition of the momentum above, we have implicitly assumed that all the particles of the system, with total mass M, are moving with the same velocity. However, if the system is made up of N particles, each one being of different mass m_i (i = 1 to N) and also moving with a different velocity 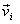, the total momentum of the system will be given as

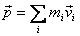
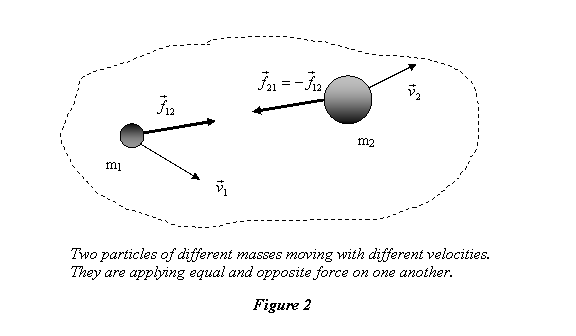
A fundamental property of momentum is now follows from the definition of force in terms of momentum. If the total force acting on a system of particles is zero, the total momentum of the system does not change with time. To see it clearly let us go back to the two particles connected by a spring (see figure 2 below). There we have

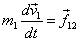
for particle 1 and

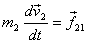
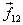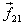for particle 2. Here is the force on particle 1 applied by particle 2. Similarly is the force on particle 2 applied by particle 1. By Newton 's third law

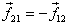
This immediately results in

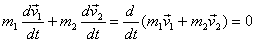
So no matter how these particles move - their individual velocities 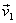or 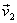may change - but as long as there is no other force on the system and Newton's third law is obeyed we are going to have

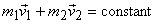
The equation above expresses the principle of momentum conservation - which is a fundamental principle of physics - in its simplest form.

Let us understand this result. If we consider both the particles together as one system, indicated by the dashed line enclosing them in the figure above, there is no force on this system. This is because although each particle is acted upon by a force applied by the other particle, on the system as a whole these two forces act in opposite directions and cancel each other, resulting in a zero net force on the system. As such the momentum of the system does not change. Thus we conclude: If the net force acting upon a system of two particles vanishes, their total momentum does not change with time . Let us now see what happens when we apply forces on each particle also. In that case we have

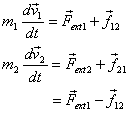
which gives

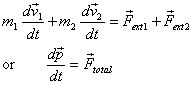
Again we see that no matter how the individual velocities change, the total momentum changes according to the equation

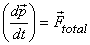
Let us now generalize this result to a system of many particles (say N ). Then we have for the i^th particle

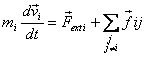
Where 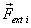is the external force on the i^th particle and 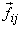is the force applied on i^th particle due to j^th particle. Summing it over i gives

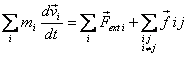
Now we can write

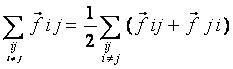
But by Newton 's third law 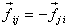which when substituted in the equation above gives

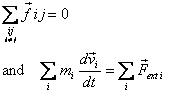
i.e., the total momentum of a system of particles changes due to only the net outside force applied on the system; the interaction between particles does not affect their total momentum. And if 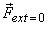i.e., there is no external force on the system,

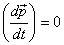
which means that the total momentum of the system is a constant. That is the statement of conservation of momentum. We will see later that when combined with the principle of conservation of energy, it becomes a powerful tool for solving problem in mechanics. For the time being let us use this principle to develop some intuitive feeling about motion of a collection of particles; looking at it as a single mass.

We now introduce you to the concept of the centre of mass (CM). To do this, let us look at the equation of motion

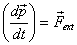
which is equivalent to

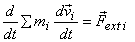
Since total mass of a collection of particles remains the same, we can divide and multiply the left-hand side of the equation above by the total mass to rewrite it as

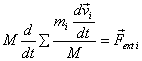
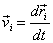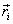Since , where is the position of the i^th particle, the above equation can also be written as

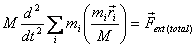
Now we introduce the position vector 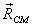for the centre of mass by writing

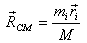
so that the equation of motion looks as follows

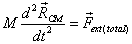
Now we interpret this equation: It says that irrespective of the interaction between the particles and their relative motion, the centre of mass of a collection of particles would always move as if it were a point particle of total mass M moving under the influence of the sum of externally applied forces on each particle, i.e., the total external force. I caution you that the equation above does not imply that all the particles are moving the same way. All it says is that they move in such a way that the motion of their CM is described as if the CM was a particle of mass M.