Let us now take a couple of standard examples involving friction similar to those solved in lecture 6.

Example 1: We put a block of 5kg on top a 10kg block. They are then attached through a massless and frictionless pulley to a mass M as shown in figure 1. The coefficient of friction between all surfaces for both static and dynamic friction is 0.5. What is the acceleration for (a) M = 20kg and (b) M = 40kg ( g = 9.8m/s² )?

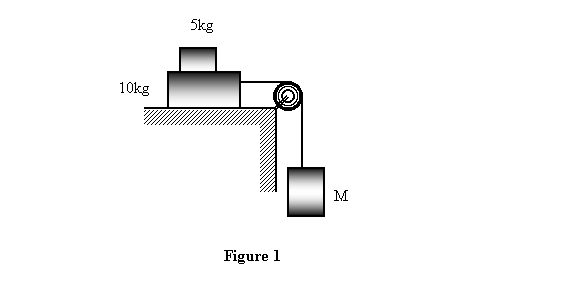
What we should see in solution of this problem is the maximum possible acceleration that the 5kg block can have, and then solve for the mass M₀ that will give this acceleration for both the 5kg and the 10kg blocks. If M is less than M₀, both the blocks will move together. On the other hand, if M exceeds M₀, the blocks will slip on each other.

To start the calculations I show in figure 2 the free body diagrams of all the masses with maximum possible friction

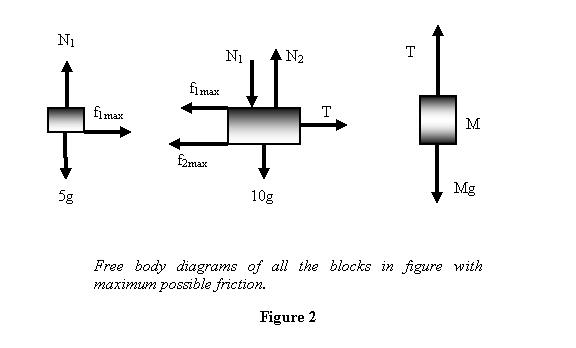
Looking at the 5kg block, we see that

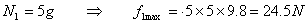
The maximum possible acceleration for the 5kg mass is

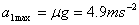
Let me now calculate M₀ corresponding to this acceleration. The corresponding equations for the 10kg block are

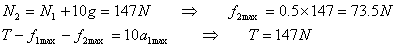
The equation of motion for the mass M then gives M₀ as follows

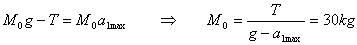
Now I answer the question asked in the problem.

(a) For 20 kg mass, let the friction between the blocks be f. Then we have

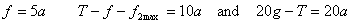
These equations lead to the acceleration of the system as follows

(b) M = 40kg. Although I have already shown you that in this case the two blocks will slide on each other. Let me show this to you again in another way. Assume that the blocks move together. In that case the acceleration of the assembly will be

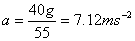
But this is larger than the maximum possible acceleration for the 5kg block, so the assembly cannot move together. Under these conditions the equations for the 10kg block and the mass M are

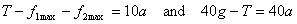
which gives

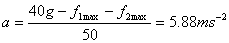
The 5kg mass of course moves with acceleration of only 4.9ms^{- 2} .

Example 2: As the second example let me take a hollow cylinder that is rotating about its axis with a constant angular speed ω . Because of this rotation a mass m on the wall of the cylinder does not slip down (see figure 3). If the coefficient of friction between the cylinder wall and the mass is µ, what is the minimum value of w for this to happen?

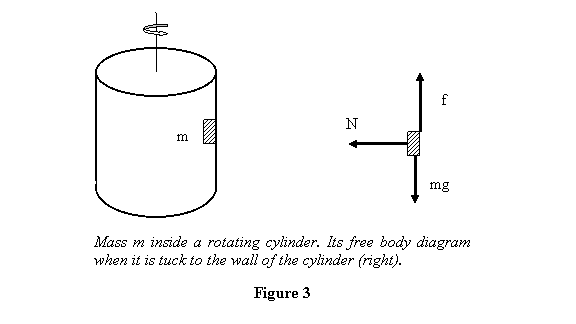
For the mass not to slip, the maximum possible friction on it should be greater than the actual frictional force that holds it against its weight. Since the problem involves rotation we will use cylindrical coordinates. The free body diagram of the mass is as given in figure 3. The mass m experiences three forces when it is stuck to the wall of the cylinder. These forces are its weight mg, the normal reaction N of the cylinder and the frictional force f . In cylindrical coordinates the acceleration of the mass is

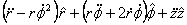
so that

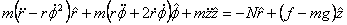
Now

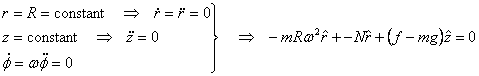
which gives

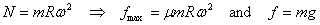
From this minimum angular speed ω_min is calculated as follows.

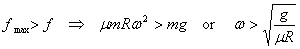
Thus 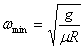.