Lecture 13
Motion with friction and drag

We have been looking at the constrained motion of particles and found that in solving the problems we make free-body diagrams and look at the motion of each subsystem independently. Then the motion of individual subsystem is linked through constraints that they impose on each other. The example that we took were Atwood's machine and a mass sliding on a wedge. However, in these examples we neglected a ubiquitous force which is the force of friction. In this lecture we take this into account and solve problems involving the friction

We would take into account two kinds of frictional forces - one that arises when two solid bodies are in contact and the other that arises when a body is moving through a liquid, the viscous force. Let us first consider the case when two solid bodies are moving against each other. A detailed discussion about the nature of frictional force and its relationship with the normal reaction has already been presented in lecture 6. We start with a review of the main points discussed there.

If there is a tendency between two bodies to slide against each other, or if one body is sliding over a surface, the friction between the two bodies resists this motion. Question is whether this is a constant force or adjusts itself. It is experimentally observed that the maximum frictional force that a surface can apply on an object is

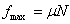
where N is the normal reaction of the surface on the body and µ is the coefficient of friction; its value is different for the static and dynamic case. Thus there are two coefficients of friction between two surfaces: static coefficient of static friction µ_s and the coefficient of dynamic friction µ_k, with the latter being smaller than the former. Further, µ_s is always observed to be less than 1. And the direction of frictional force is such that it opposes the motion or the tendency to move.