Let us now apply the procedure outlined above to slightly
more difficult examples.
Example 1: There are three massless
and frictionless pulleys P1, P2 and P3. P1 and P2 are
fixed and P3 can move up and down, as shown in figure
5. A massless rope R1 passes over the pulleys as shown
and two masses m1 and m2 attached
at its ends. A third mass m3 is hanging from P3 by a
rope R2 of fixed length. Find the acceleration of the
three masses.
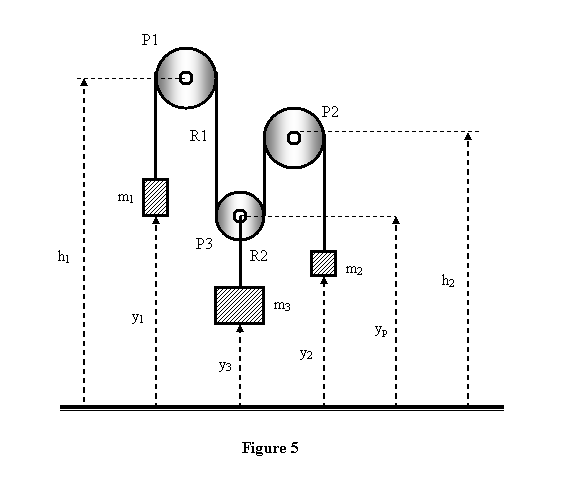
In figure 5 we have also shown the distances of different
pulleys and masses from the ground, with the vertically
up direction taken to be positive. The heights h1 and
h2 of pulleys P1 and P2, respectively, are
fixed whereas height yp of pulley P3 can change. We go
about solving the problem according to the steps given
above.
Step 1: We identify two constraints and the forces of
constraints as: rope R1 has fixed length with the force
of constraint being tension T1 in
the rope. The other constraint is that rope R2 has fixed
length with the tension T2 in the
rope as the constraint force. Because of massless pulleys
and ropes and frictionless surfaces T1 is the same throughout
rope R1.
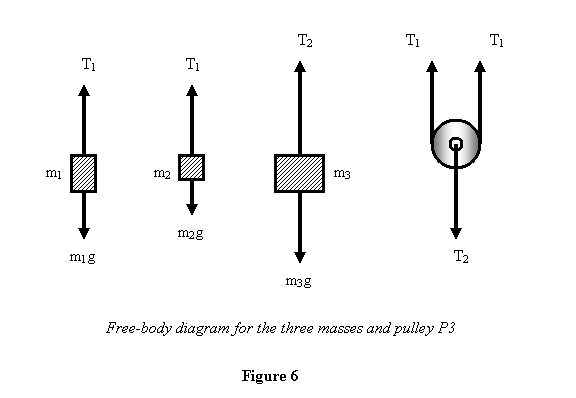
Step 2 : Make free-body diagrams of the subsystems. We
consider only those subsystems that can move. Thus we
make free-body diagram of each mass and the pulley P3
as shown in figure 6.
Step 3 : By looking at the free-body diagrams, write equations
of motion for each subsystem. In terms of the distances
shown in figure 5, we get
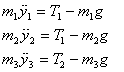
and because the pulley is massless
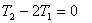
Thus equations of motion give four equations. However
there are six unknowns viz. 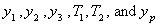 .
Their number exceeds the number of equations obtained
so far by two. .
Their number exceeds the number of equations obtained
so far by two.
Step 4 : The additional two equations are provided by
the constraint equations. The constraint that rope R1
is of fixed length is expressed as (see figure 5 for
the variables used)
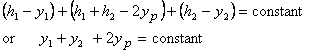
Differentiating this equation twice with respect to time
gives
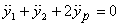
The second constraint that rope R2 is of fixed is equivalent
to
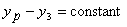
which upon differentiating gives
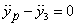
Thus the equations that describe the motion of the system
fully are:
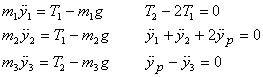
I will leave Step 5 – that is solving the equations -
for you to do but give you partial answer. It is
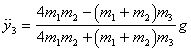
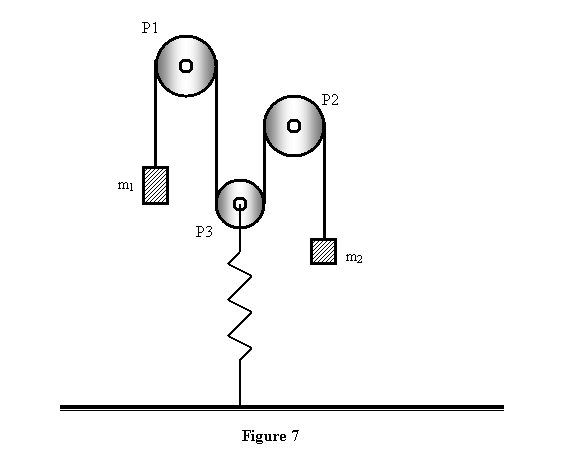
I would now like you to try a similar problem but with
slight difference. Let us attach the centre of the third
pulley to a spring of spring constant k (see
figure 7). Then find the equations of motion for the
two masses and solve them.
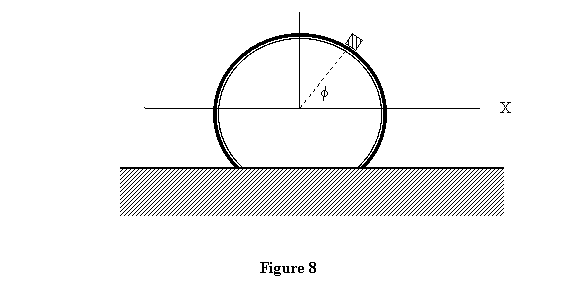
Example 2 : As another example of constrained
motion we take a small block of mass m sliding
down on a cylindrical surface from its top (figure 8).
The question we ask is at what angle from the horizontal
would the mass slide off the surface of the cylinder.
Since this problem involves motion along a circular path
I would use planar polar coordinates. I take the origin
at the centre of the cylinder and let the x-axis be along
the horizontal and y-axis along the vertical. Assume
that the radius of the cylinder is R . The constraint
in this problem is that r = constant = R. The
corresponding constraint force is the normal reaction
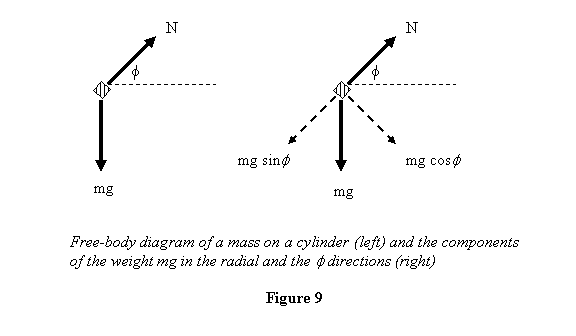
N of the cylindrical surface on the block. The free-body
diagram of the mass on the cylinder is shown in figure
9.
We now write the equations of motion in the planar polar
coordinates. That gives in the 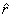 direction direction
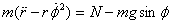
and in the 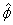 direction direction
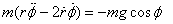
We again have three variables 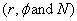 but
only two equations. The third equation is provided by
the equation of constraint i.e. but
only two equations. The third equation is provided by
the equation of constraint i.e.
r = constant = R
which gives
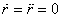
With this the equations to be solved are

To solve these we use
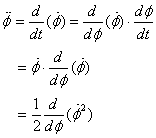
Substituting this in the equation for 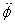 above
gives above
gives
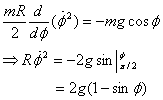
This when substituted in the equation for 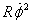 leads
to leads
to
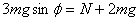
The point when the mass slips off the cylinder is where N becomes
zero. So the corresponding 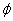 is
given by is
given by
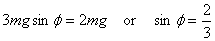
Example 3: Let us take one more example
of constrained motion when two bodies are involved. I
put a block of mass m on a wedge of mass M
with wedge angle θ (see figure 10). The wedge is free
to move on a frictionless plane. There is no friction
also between m and M . We wish to
find the resulting motion.
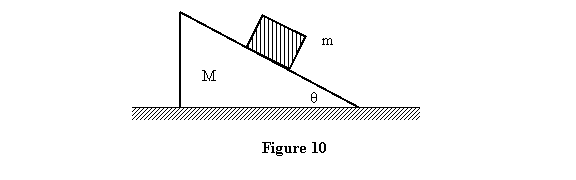
There are clearly two subsystems, the masses m and M .
There are two constraints in the system. Constraint one
is that the mass m moves along the edge of
the wedge so its x and y components
are not independent. The other constraint is that the
wedge moves only in the x direction. The constraint forces
are obviously the normal reaction N1 on
mass m by
the wedge and the normal reaction N2 on the
wedge by the ground. The free-body diagrams for the two
subsystems are as shown in figure 11.
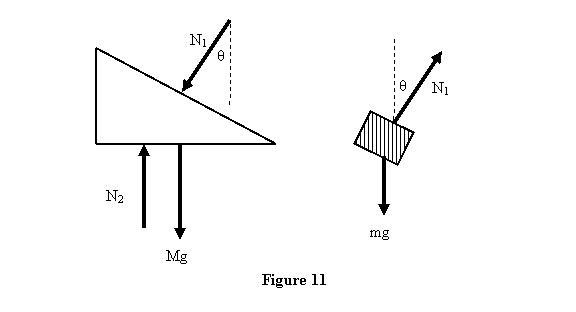
Notice that in the free-body diagram of the wedge, there
is no mg of block. It is all accounted for
by N1. To set up the equations of
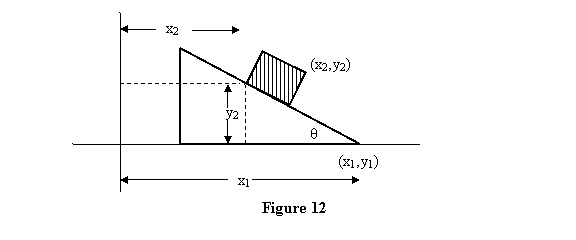
motion, let us choose our co-ordinates system a follows
(see figure 12): Let the coordinate of the right-hand
side lower corner of the wedge be given the co-ordinates
(x1 y1 ) and let the co-ordinates
of the block be (x2 y2 ).
The equations of motion in terms of these coordinates
are:
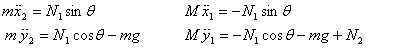
For the six variables - 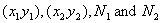 -
of the system, we need two more equations, which are
provided by the constraints equations. These are -
of the system, we need two more equations, which are
provided by the constraints equations. These are

and
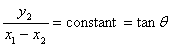
which gives
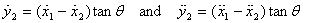
Thus the equations to be solved are
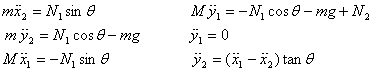
These equations can now be solved to get all the variables
as a function of time. That task is left for you. I'll
leave you with answers for N1 :
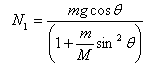
|