So far we have discussed one kind of frictional force where two solid bodies are in contact. We now learn to deal with the drag force which is experienced when a body is moving through gas or a liquid. This force arises due to viscosity of the fluid. To the lowest order in the velocity 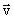 of the moving body, the drag force is approximated by of the moving body, the drag force is approximated by
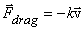
that is, it is a force in the direction opposite to the velocity and its magnitude is proportional to the speed. So the equation of motion in presence of drag force will read
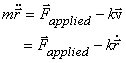
If we write it in its component form we have
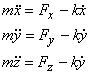
These formulae are valid when the speed of the object is not very large; at large speeds the drag force becomes proportional to the square of the velocity. The simplest example of the effect of drag is the falling raindrops. Although falling from great heights, they do not hit us with very large speed because of the drag force on them.
As an object falls vertically through a liquid/gas, the drag force on it increases with its speed. At a certain speed - when the drag force equals the weight of the object - it stops accelerating further and therefore moves with a constant speed. This speed is known as the terminal speed or terminal velocity. Assuming drag force to be linearly dependent on velocity, let us estimate the terminal speed of an object when it falls through a liquid of viscosity η. Let the vertically downward direction be y, then
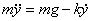
But the object will stop accelerating, i.e. 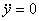 , after attaining the terminal speed. Thus at the terminal speed , after attaining the terminal speed. Thus at the terminal speed 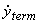
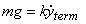
which gives
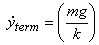
That is the terminal speed of the object. To estimate the terminal speed we need to know what k is. For a spherical object of radius a moving with low speeds, stokes formula gives the drag force to be
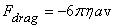
If the object is made of a material of density ρ, the terminal speed comes out to be
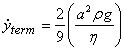
Let us estimate what will be the terminal speed of a rain drop of 2mm radius. With the viscosity of air 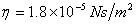 , we get , we get
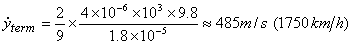
This is too high compared to the observed speeds of about 20 kmph to 5 kmph. Obviously the dependence of drag force on raindrops has higher power dependence on their speeds. In this lecture we will however restrict ourselves to those cases where the drag force depends linearly on the speed i.e. 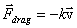 . We now solve examples involving such drag force. . We now solve examples involving such drag force.
Example 3 : An object is thrown in a fluid with initial speed v0. Find its speed and the distance traveled by it as a function of time.
Assuming the motion to be in x direction, the equation of motion is
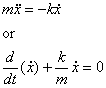
You can easily check that the solution is
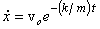
So that the speed initially is v0 and it decreases exponentially with time. The plot of speed versus time looks like that given below
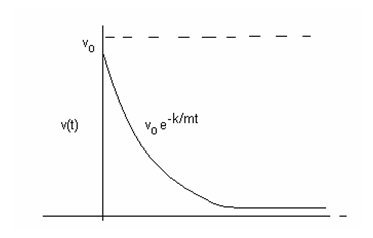
What about the distance traveled by the object? That is obtained by integrating the speed with respect to time and is
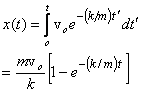
So that the distance traveled looks like
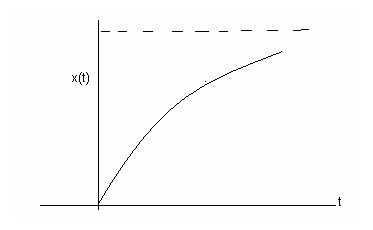
Thus as  , the body will stop after traveling a distance of , the body will stop after traveling a distance of
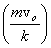
Of course as 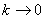 , the distance becomes larger and larger. , the distance becomes larger and larger.
Example 4 : We now consider one-dimensional motion of a particle which is moving under the influence of a constant applied force in a medium applying a drag force. Motion of a particle thrown up or falling down is one such example. The equation of motion in this case is
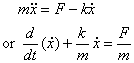
Let us take the force to be F and the initial speed of the particle to be zero. Without the term 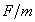 on the right-hand side, the solution of the equation above was on the right-hand side, the solution of the equation above was 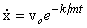 which is, in the language of differential equations, the solution of the homogeneous equation i.e., equation with 0 on the right-hand side. To get the general solution, we add to the homogeneous solution the particular solution corresponding to which is, in the language of differential equations, the solution of the homogeneous equation i.e., equation with 0 on the right-hand side. To get the general solution, we add to the homogeneous solution the particular solution corresponding to 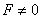 . The particular solution is . The particular solution is
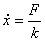
So that the general solution for the velocity is
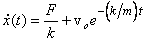
Here v0 is some constant (not the initial velocity, which is given to be 0). If we start with 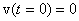 we get we get
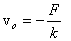
which gives
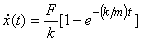
The plot of velocity versus time looks as follows

with the terminal speed being 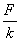 . The next question we ask if the solution goes to the standard solution . The next question we ask if the solution goes to the standard solution 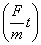 of particle moving with a constant acceleration when k=0. From of particle moving with a constant acceleration when k=0. From 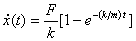 we get an answer of 0/0 so we have to be careful in taking k = 0 . Recall that the solution was obtained by assuming k ≠ 0 because we have been dividing by k . Thus for the k=0 case we should take the limit of k → 0 . Doing that we find we get an answer of 0/0 so we have to be careful in taking k = 0 . Recall that the solution was obtained by assuming k ≠ 0 because we have been dividing by k . Thus for the k=0 case we should take the limit of k → 0 . Doing that we find
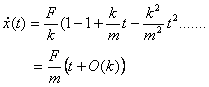
Now k → 0 gives 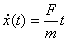 which is the correct answer. We now calculate the distance x(t) traveled by the object as a function of time. which is the correct answer. We now calculate the distance x(t) traveled by the object as a function of time.
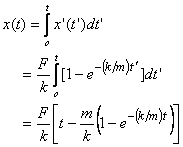
You can see that t → ∞ the distance is given as
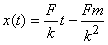
so at large times it increases linearly with the terminal speed.
For t → 0 it is
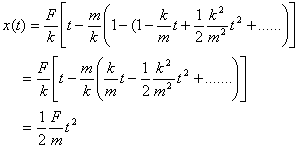
This is easily understood as initially there is no drag due to small initial speed and the distance is given by the formula for uniform acceleration. Combining the two limiting cases we see that the plot of x(t) versus time looks like
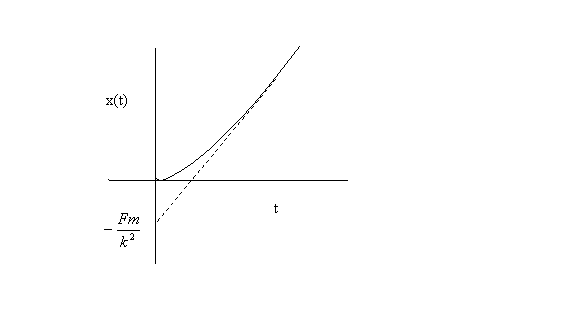
I'll leave it as an exercise that as k → 0 , we recover the familiar result 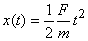 Also I would like you to solve for the velocity and height of a ball thrown up with an initial speed v 0 when drag of air is taken into account. Also I would like you to solve for the velocity and height of a ball thrown up with an initial speed v 0 when drag of air is taken into account.
Next we analyze the effect of drag on the projectile motion in the gravitational field. In this case, we have a projectile shot with initial speed v0 at an angle θ0 from the horizontal and we want to find to subsequent motion. The equations of motion are (taking vertically up direction as the y-direction)
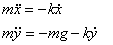
We have already solved these equations above, so the speed and distance in the x-direction is given as
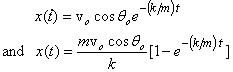
The equation of motion in the y-direction is
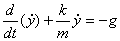
Its solution with the initial condition 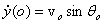 is is
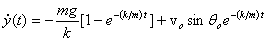
I give you an exercise now: find at what time s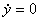 ? Show that this time correctly goes to ? Show that this time correctly goes to 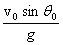 when k = 0 . Integrating the speed, we get the height y(t) as a function of time. It is given as when k = 0 . Integrating the speed, we get the height y(t) as a function of time. It is given as
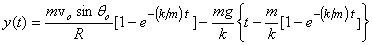
Now to get the trajectory one calculates x(t) and y(t) separately and plots y versus x . I give you some of these for a given 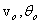 but varying k. We take v0 = 100m/s and θ0 = 45º . For no drag situation we get the range R = 1010m and the highest point of the projectile to be at h = 254m . When a drag coefficient of k = 0.1 is introduced we get R = 495m and h = 175m , a reduction of about 50% in the range and 30% in the height. For k = 0.2 we get R = 313m and h = 135m, giving a further reduction of about 40% in the range and 20% in the height from the corresponding k = 0.1 values. Notice when drag force is introduced, the range gets affected much more than the height. The corresponding trajectories are shown below. but varying k. We take v0 = 100m/s and θ0 = 45º . For no drag situation we get the range R = 1010m and the highest point of the projectile to be at h = 254m . When a drag coefficient of k = 0.1 is introduced we get R = 495m and h = 175m , a reduction of about 50% in the range and 30% in the height. For k = 0.2 we get R = 313m and h = 135m, giving a further reduction of about 40% in the range and 20% in the height from the corresponding k = 0.1 values. Notice when drag force is introduced, the range gets affected much more than the height. The corresponding trajectories are shown below.
One interesting question we may ask is: for zero drag the maximum range is obtained for θ = 45º. If we include drag, should the angle be larger than or less than 45º for obtaining maximum range? Since x-component of the velocity is now decreasing one intuitively feels that the projectile should be given larger speed in the x-direction for maximum range. Thus the projectile should be fired at an angle less than 45º. This is easily understood from the calculations presented above. As we saw in those calculations, for k ≠ 0 the motion in y direction does not get affected as much as it does in the x-direction. This also suggests that for maximum range we fire the projectile at an angle slightly less than 45º giving it a lager velocity in x-direction. One can also think of it slightly differently. When the particle is shot up drag force is large (because of the initial speed) and also both the gravitational force and drag are working in the same direction. So the partial takes longer to move up the same height than it does in coming down. Since x-velocity is larger in the beginning, the projectile should cover as much distance as possible while ascending than when it is coming down (the x-component may well vanish by that time) This implies that θ0 should be smaller than 45º.
What we have done so far is to include the simplest form of drag force in solving for the trajectories of motion. However, as the speed increases drag force may also include higher powers of velocity i.e. it may take the form
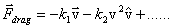
where 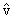 is the unit vector in the direction of the velocity. This is written here to show that force is opposite to the velocity vector. In such cases the corresponding differential equation become non-linear in v and getting the solution becomes difficult, necessitating the use of numerical methods. Some problems though do allow analytic solutions. I end this lecture by giving you one such problem to solve. is the unit vector in the direction of the velocity. This is written here to show that force is opposite to the velocity vector. In such cases the corresponding differential equation become non-linear in v and getting the solution becomes difficult, necessitating the use of numerical methods. Some problems though do allow analytic solutions. I end this lecture by giving you one such problem to solve.
Exercise : Throw a ball up will initial velocity 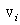 and let the force of drag be and let the force of drag be 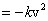 . Find the final speed . Find the final speed 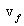 of the ball when it hits the ground. Also find the height that it goes up to. of the ball when it hits the ground. Also find the height that it goes up to.
|