A rod at an angle from the axis of rotation passing through its centre: This is shown in figure 4. The length of the rod is l and its mass m . It is at an angle θ   from the axis of rotation.

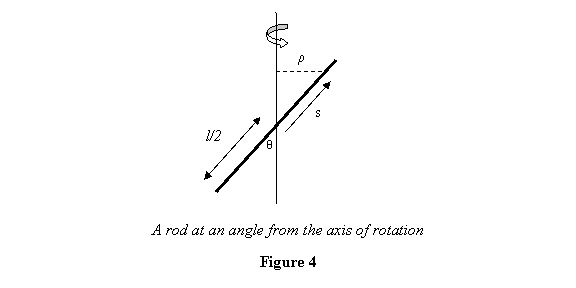
We take a small mass element of length ds at a distance s from the origin. It is at a distance 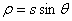from the axis of rotation. Then

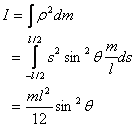
Thus for a rod rotating about its perpendicular passing through its centre is .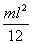

Exercise: Calculate the moment of inertia of a disc rotating about an axis passing through its centre and perpendicular to it.

 

Moment of inertia of disc about one of its diameters: Shown in figure 5 is a disc of mass M and radius R rotating about its diameter which lies on the y-axis.

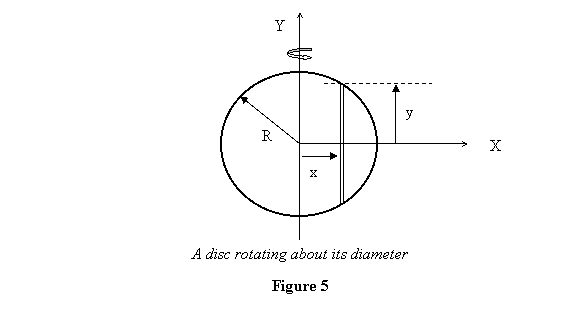
To calculate the moment of inertia I take a strip of lengths width dx at distance x from the y-axis, the axis of rotation. Its mass is 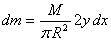(see figure 5). Thus

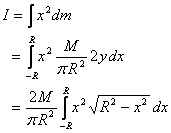
The integration can be carried out easily by substituting 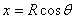and gives

 

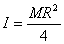
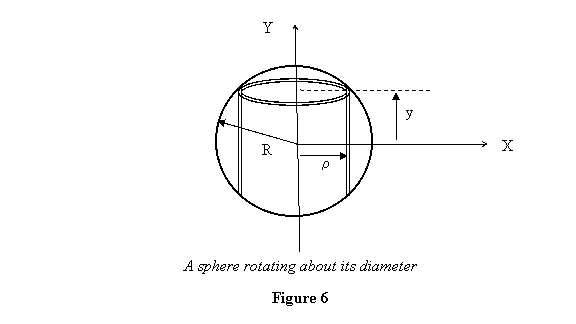
Moment of inertia of a sphere about one of its diameters: A sphere of mass M and radius R is shown in figure 6. To calculate its moment of inertia, we take a cylindrical shell of radius ρ
and thickness dρ (see figure 6). The mass of this shell is given by

 

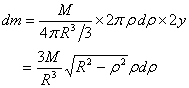
Therefore the moment of inertia is

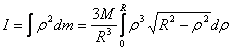
By substituting 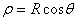, this is an easy integral to perform and gives the result
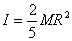