Let us now recapture what we have done so far. We have looked at the angular momentum of a body rotating about a fixed axis. We find that angular momentum L_Z about an axis (denoted as the z-axis) is given as L_Z = I_Z ω and, depending upon the sense of rotation, can take positive as well as negative values. We have also calculated I_Z for some standard objects about an axis. We now go on to study the equation of motion satisfied by L_Z . The equation satisfied by L_Z is

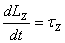
wher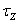e is the component of the external torque along the axis of rotation. If the external torque is zero, the angular momentum is conserved. You can observe the effect of conservation of angular momentum easily at home.

Sit on a revolving chair holding a brick (or something similar) in each of your hands and keep your arms stretched. Start revolving the chair and then pull your arms in. You will observe that you start revolving much faster. This happens because when you pull the arms in, the masses that you are holding come closer to the axis of rotation resulting in a reduction in the value of the moment of inertia. However, since there is no external torque on the system, the angular momentum cannot change. Thus if the moment of inertia decreases, the angular speed must increase in order to keep L = Iω constant. This is precisely what you observe. You should also repeat the experiment holding different weights. When do you observe the rotational speed to increase the largest? Let us now solve an example of applying the angular momentum conservation principle.

 

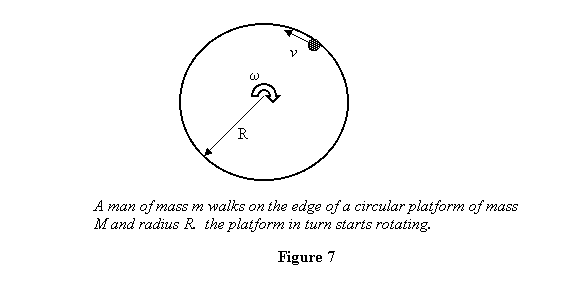
Example: A man starts walking on the edge of a circular platform with a speed v with respect to the platform (see figure 7). The platform is free to rotate. What is the rotational speed of the platform? Mass of the platform is M , its radius is R and the mass of the man is m .

Since there is no external torque, the angular momentum of the system about the axis of rotation must be conserved. Thus as the man starts walking, the platform starts rotating the other way. Since the speed of man with respect to the platform is v , his speed in the ground frame would be   (v – ωR) . Thus the angular momentum of the man is

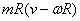
At the same time, the angular momentum of the platform is

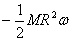
where the minus sign shows that the angular momentum of the platform is in the direction opposite to that of the man's angular momentum. By conservation of angular momentum

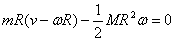
which gives

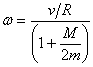
Having learnt about the angular momentum, its equation of motion and the conservation of angular momentum for rotations about a fixed axis, we now discuss the kinetic energy and the work-energy theorem for a rigid body rotating with angular speed w about a fixed axis.