Kinetic
energy and work-energy theorem for a rigid-body rotating
about a fixed axis: The
kinetic energy of
a rigid body rotating
with angular speed ω is
obtained by calculating
the energy of small mass
element in the body and
adding it up. This mass
element is rotating in
a plane perpendicular
to the axis of rotation.
This gives (using
the notation of figure
2)

The corresponding work-energy theorem for the motion considered
here is that the change in kinetic energy is equal to
the work done on the body. Let us first calculate the
work done on a body, which can only rotate about an axis,
when an external force is applied on it. To do this,
I would first like you to prove a result (look at figure
2 for reference): when a body rotates by an angle Δθ about
an axis in the unit vector direction 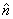 ,
the corresponding change in position of a particle in
the body at position vector ,
the corresponding change in position of a particle in
the body at position vector 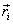 is is
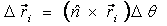
The total work done on the body by a net external force
composed of forces 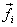 acting
at each point is acting
at each point is
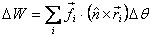
By using 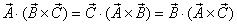 ,
we can write the work done as ,
we can write the work done as
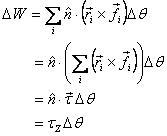
where τZ is the component of the external torque
along the axis of rotation. Thus the total work done
is
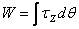
Now the work energy theorem can be expressed as follows:
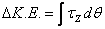
This pretty much concludes what all I have to say about
the rotations about a fixed axis. One question that may
be asked at this point is: Why is it what describing
dynamics in term of angular momentum, torque etcetera
rather than momentum and force is more useful in discussing
rotational motion. This is because in rotational motion,
force, momenta etcetera are distributed and taking their
moments by considering the angular momenta and torques
automatically takes care of this distribution. We conclude
this lecture by drawing a comparison between linear and
rotational motion about a fixed axis.
Linear
motion |
Rotational
motion about a fixed axis |
Momentum
p |
Angular
momentum L |
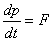
|
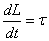
|
Impulse 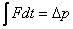 |
Impulse 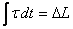 |
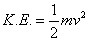
|
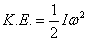
|
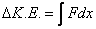
|
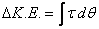
|
This correspondence will help in understanding and getting
relationships to solve most of the problems involving
rotations about a fixed axis, particularly if you have
solved many problems involving linear momentum.
|