Lecture
12
Motion with constraints
In this lecture we are going to deal with motion of particles
when they move under constraints applied on their motion.
Of course the motion is determined by Newton 's second
law i.e., by solving the equation of motion
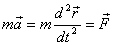
where 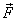 is
the total force – which is the sum of the externally
applied and those arising from other particles as well
as the constraints in the system - acting on a body of
mass m and is producing an acceleration is
the total force – which is the sum of the externally
applied and those arising from other particles as well
as the constraints in the system - acting on a body of
mass m and is producing an acceleration 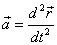 .
Recall from lecture 9 that constraints are the
restrictions applied on the movement of a body by various
means and are brought about by constraint forces .
For example, I may restrict the body to move along a
straight wire (see figure 1). In that case the component
of .
Recall from lecture 9 that constraints are the
restrictions applied on the movement of a body by various
means and are brought about by constraint forces .
For example, I may restrict the body to move along a
straight wire (see figure 1). In that case the component
of 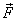 only
along the wire will affect the motion of the mass (if
there is no friction) and its perpendicular component
will be nullified by the normal reaction of the wire,
which is the constraint force in this case. As another
common example of constrained motion take the motion
of two masses at the end of a rope going over a frictionless
pulley (Atwood's machine) also shown in figure 1. only
along the wire will affect the motion of the mass (if
there is no friction) and its perpendicular component
will be nullified by the normal reaction of the wire,
which is the constraint force in this case. As another
common example of constrained motion take the motion
of two masses at the end of a rope going over a frictionless
pulley (Atwood's machine) also shown in figure 1.
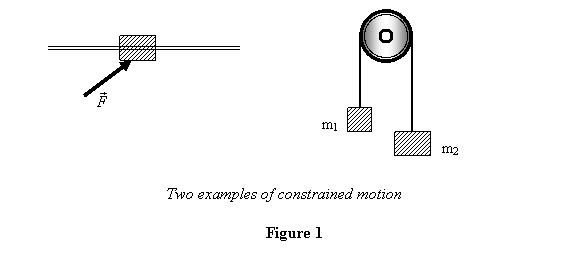
In
this case also, the motion of one mass is determined
by not only by the gravitational force on it alone but
also by the weight of the other mass. Thus the two masses
are not fully free to move under their own weight and
the motion is constrained. The constrained is brought
about through tension in the rope, which is then the
constraint force.
We have seen two simple examples of constrained motion.
We make an observation that constraints can be caused
either by restricting the motion externally, as was the
case for a mass on a wire, or by the presence of other
bodies that are themselves moving, as in the example
of two masses over a pulley. In lecture 9 we had introduced
these concepts and stopped at that. However, for obtaining
the positions and velocities of particles under constraints,
we wish to express these constraints mathematically and
account for them while solving the equations of motion.
This is what this lecture is going to be about.
|