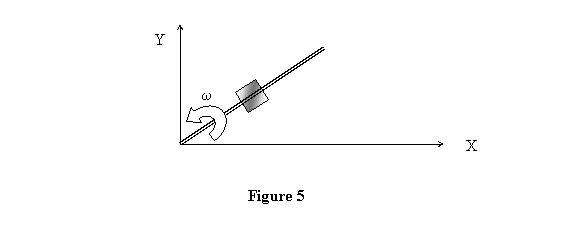
Example 1: A bead of mass m can
slide without friction on a straight thin wire moving
with constant angular speed 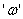 in
a horizontal plane (figure 5). If we leave the bead with
zero initial radial velocity at in
a horizontal plane (figure 5). If we leave the bead with
zero initial radial velocity at 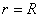 ,
we wish to describe its subsequent motion and also find
the horizontal force applied by the wire on the bead. ,
we wish to describe its subsequent motion and also find
the horizontal force applied by the wire on the bead.
To see the usefulness of polar coordinates, try to write
equations of motion for the bead in the Cartesian coordinates.
This I leave for you to do. We solve the problem using
polar co-ordinates. Thus at any instant the acceleration
is given by the formula
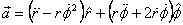
We emphasize that the expression above gives the components
of the acceleration along the radial and the f directions
which are not fixed in space but are changing continuously.
It is given that 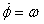 (a
constant) which also means that (a
constant) which also means that 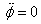 .
The acceleration of the bead on the wire is therefore .
The acceleration of the bead on the wire is therefore
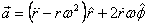
Since there is no friction, the wire does not apply any
radial force on the bead. Therefore
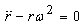
You can check by substitution that the solution for the
equation above is
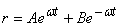
where A and B are two constants to be determined from
the initial conditions. Differentiating the equation
above gives
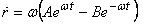
Thus acceleration perpendicular to wire is
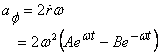
So the horizontal force applied by wire is
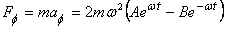
Of course because the unit vectors employed change direction
continuously, the force above is also in different directions
at different times with the magnitude given by the expression
above. To determinate A and B, we substitute t = 0 in
the expressions derived for the radius and the radial
speed and equate them to their vales given at that time.
This gives
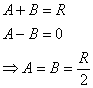
This leads to the answer
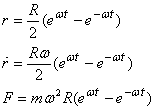
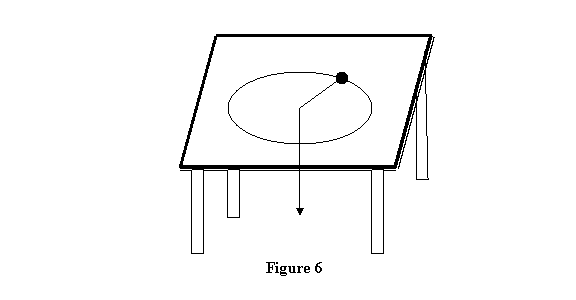
Example 2: A particle, tied to a string,
is moving on a smooth frictionless table in a circle
of radius r0 with an angular speed ω0.
The string is pulled in slowly through a hole in the
middle of the table with constant speed V.
We want to find the change in its speed as a function
of time and also the force required for the string to
be pulled (figure 6).
The mass, when pulled in, is moving under the influence
of an inwardly directed radial force 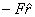 .
Although the force keeps changing its direction depending
upon where the particle is, it always remains radial.
The expression for the acceleration of the particle in
the polar coordinates is .
Although the force keeps changing its direction depending
upon where the particle is, it always remains radial.
The expression for the acceleration of the particle in
the polar coordinates is
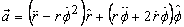
Since it is given 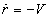 ,
which means ,
which means 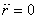 ,
and the force is only in ,
and the force is only in 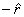 direction,
we have direction,
we have
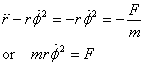
Since there is no force component in the Φ direction,
we have
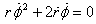
Multiply both sides of this equation by r to
get
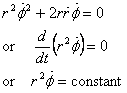
Since 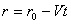 ,
the equation above gives ,
the equation above gives
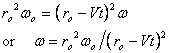
The force 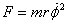 pulling
the string in is therefore pulling
the string in is therefore
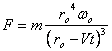
In solving this example, we see that for forces in radial
direction 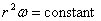 ,
which is nothing by a statement of the conservation of
angular momentum. We will discuss it more later when
we study angular momentum. ,
which is nothing by a statement of the conservation of
angular momentum. We will discuss it more later when
we study angular momentum.
After introducing the planar polar coordinates, we nor
briefly describe what are the other coordinate systems
in three dimensions. A natural extension of planar coordinates
in the cylindrical coordinate system. This arises when
we add the third-z direction to planar polar coordinates.
See figure 7.
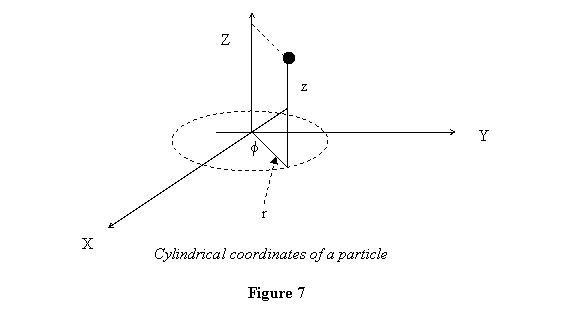
The position of a particle is described by 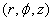 with
the corresponding unit vectors being with
the corresponding unit vectors being 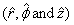 .
In this case the .
In this case the 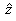 unit
vector is a constant and unit
vector is a constant and 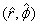 are
given as in the planar polar co-ordinates so that are
given as in the planar polar co-ordinates so that
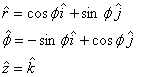
Thus the expressions for all the quantities are similar
to those for planar polar co-ordinates except that 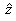 direction
is also added. As a result, direction
is also added. As a result,
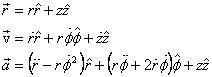
We now introduce another set of coordinates, the spherical
polar coordinates, in three dimensions. A point in these
coordinates is specifically by its distance from the
centre r , the angle θ that the line
joining the point to origin makes with the z-axis and
the angle Φ that the projection of this line
on the (xy) plane makes with the x-axis. Thus a point
is specified by 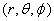 (see
figure 8). (see
figure 8).
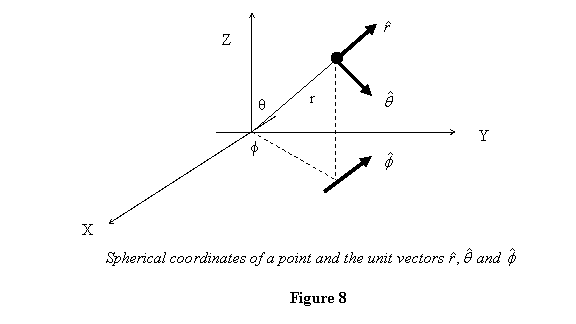
Thus 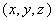 co-ordinates
for a point co-ordinates
for a point  are are
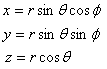
The unit vectors are given as 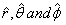 with with
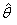 unit
vector points in a direction below the (xy) plane making
an angle unit
vector points in a direction below the (xy) plane making
an angle 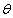 from
the (xy) plane. So it is given as from
the (xy) plane. So it is given as
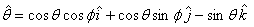
And 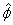 is
in the (xy) plane and is given as is
in the (xy) plane and is given as
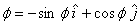
which is the same as for planar polar coordinates. As
is clear, the unit vectors in this case are also position
dependent and change as the particle position changes.
This affects the expression for velocities and acceleration
when they are expressed in spherical coordinates.
Let us evaluate the time derivatives of 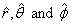 geometrically.
The unit vector geometrically.
The unit vector 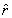 does
not depend on r but changes with θ . This gives does
not depend on r but changes with θ . This gives
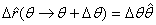
Similarly when θ is fixed and Φ changes, we
get
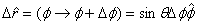
When we combine the two results we get
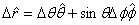
which gives
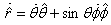
Thus the expression for velocity in spherical coordinates
is
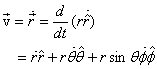
We leave the calculation of  and
the acceleration as an exercise. We end this brief introduction
to spherical coordinates by noting that spherical polar
coordinates can be those of as two plane polar coordinates
systems : one the plane of radius vector and the z-axis
with and
the acceleration as an exercise. We end this brief introduction
to spherical coordinates by noting that spherical polar
coordinates can be those of as two plane polar coordinates
systems : one the plane of radius vector and the z-axis
with 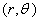 as
planar coordinates and the other the (xy) plane with as
planar coordinates and the other the (xy) plane with 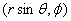 as
the planar polar coordinates. as
the planar polar coordinates.
|