Lecture
11
Motion in a plane: Introduction
to polar coordinates
So far we have discussed equilibrium of bodies i.e. we
have concentrated only on statics. From this lecture
onwards we learn about the motion of particles and composite
bodies and how it is affected by the forces applied on
the system. Thus we are now starting study of dynamics.
When we describe the motion of a particle, we specify
it by giving its position and velocity as a function
of time. How the motion changes with time is given by
the application of Newton's IInd Law. One
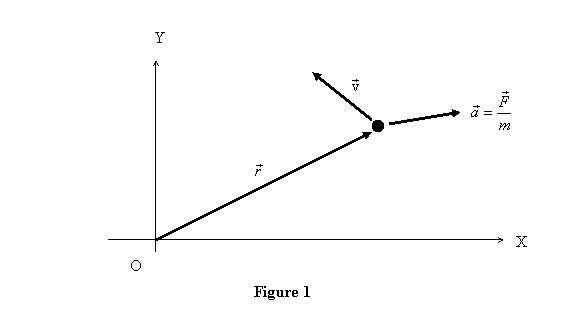
such particle at position 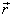 moving
with velocity moving
with velocity 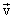 and
acted upon by a force and
acted upon by a force 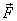 is
shown in figure 1. The force is
shown in figure 1. The force 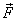 gives
rise to an acceleration gives
rise to an acceleration 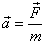 .
Notice that in general the position, the velocity and
the acceleration are not in the same direction. .
Notice that in general the position, the velocity and
the acceleration are not in the same direction.
Each of these vectors is specified by giving its component
along a set of conveniently chosen axes. For a particle
moving in a plane, if we choose the Cartesian coordinate
system (x-y axes) then the position is given by specifying
the coordinates (x, y), velocity by its components 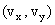 and
acceleration by its components and
acceleration by its components 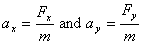 .
These are related by the relationship .
These are related by the relationship
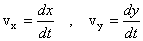
and
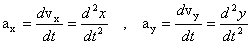
These expressions are easily generalized to three dimensions
by including the z-component of the motion also. However,
in this lecture we will be focusing on motion in a plane
only. With these components the equations of motion to
be solved are
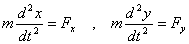
Coupled with the initial conditions solutions of these
equations provide the velocity and position of a particle
uniquely. However, the Cartesian system of coordinates
is only one way of describing the motion of a particle.
There arise many situations where describing the motion
in some other coordinate system i.e., taking components
along some other directions is move convenient. One such
coordinate system is polar coordinates. In this lecture
we discuss the use of this system to describe the motion
of a particle. To introduce you to polar coordinates
and how their use may make things easy, we start with
the discussion of a particle in a circle.
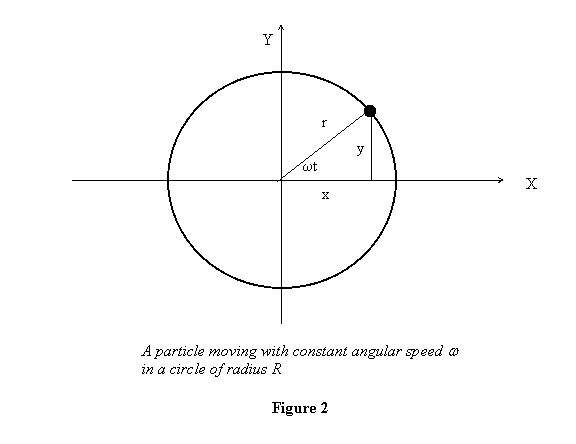
Consider a particle is moving with a constant angular
speed ω in a circle of radius R centered
at the origin (see figure 2). Its x and y coordinates
are given as
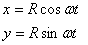
with both x and y being functions
of time (see figure 2).
On the other hand, if we choose to give the position of
the particle by giving its distance r from
the origin and the angle Φ that
the line from the origin to the particle makes with x-axis
in the counter-clockwise direction, then the position
is given as
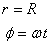
In this coordinate system, r is a constant and Φ a
linear function of time. Thus there is only one variable
that varies with time whereas the other one remains constant.
The motion description thus is simpler. These co-ordinates 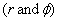 are
known as the planar polar coordinates. As expected, these
coordinates are most useful in describing motion when
there is some sort of a rotational motion. We will therefore
find them useful, for example, in discussing motion of
planets around the sun rotating bodies and motion of
rotating objects. are
known as the planar polar coordinates. As expected, these
coordinates are most useful in describing motion when
there is some sort of a rotational motion. We will therefore
find them useful, for example, in discussing motion of
planets around the sun rotating bodies and motion of
rotating objects.
So to start with let us set up the unit vectors is polar
co-ordinates ( r, Φ ) . Given a
point 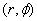 ,
the unit vector ,
the unit vector 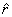 is
in outward radial direction and has magnitude of unity.
The Φ unit
vector is also of magnitude unity and is perpendicular
to is
in outward radial direction and has magnitude of unity.
The Φ unit
vector is also of magnitude unity and is perpendicular
to 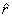 and
in the direction of increasing Φ (see
figure 3). Obviously the dot product and
in the direction of increasing Φ (see
figure 3). Obviously the dot product 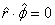 .
In term of the unit vectors in x and y direction
these are given as .
In term of the unit vectors in x and y direction
these are given as
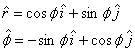
As is clear from these expression the direction of 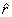 and Φ is
not fixed but depends on the angle Φ. On the
other hand, it does not depend on r. If we go along a
radius, and Φ is
not fixed but depends on the angle Φ. On the
other hand, it does not depend on r. If we go along a
radius, 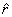 and Φ remain
unchanged as we move (recall that two parallel vectors
of same magnitude are equal). But that is not the case
if Φ is
changed. and Φ remain
unchanged as we move (recall that two parallel vectors
of same magnitude are equal). But that is not the case
if Φ is
changed.
The position a of a particle in polar co-ordinates to
given by writing
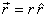
As particle moves about, 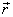 changes.
Does the mean that the velocity changes.
Does the mean that the velocity
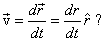
The answer is no. As already discussed 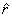 is
a function of Φ, the angle from the x-axis.
Thus as a particle moves such that the angle Φ changes
with time, the unit vector is
a function of Φ, the angle from the x-axis.
Thus as a particle moves such that the angle Φ changes
with time, the unit vector 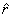 also
changes. Its derivative with respect to time is therefore
not zero. Thus the correct expression for also
changes. Its derivative with respect to time is therefore
not zero. Thus the correct expression for 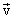 is is
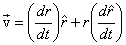
Let us now calculate 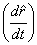 .
As already stated, .
As already stated, 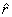 does
not change as one moves radically in or out. Thus does
not change as one moves radically in or out. Thus  changes
only if Φ changes.
Let us now calculate this change (figure 4) changes
only if Φ changes.
Let us now calculate this change (figure 4)
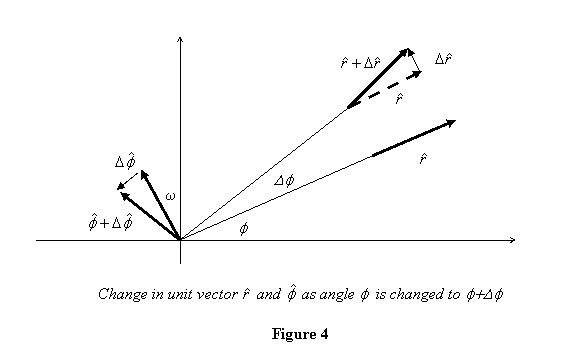
As is clear from the figure
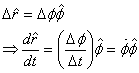
where the dot on top of a quantity denotes its time derivative.
The expression above can also be derived mathematically
as follows:
 
Thus the velocity of a particle is given as
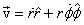
We note that the unit vectors in polar coordinates keep
changing as the particle moves because they are given
by the particles current position. Thus even if a particle
were moving with a constant velocity, the components
of velocity along the radial and the directions
will change. Let us calculate the velocity of a particle
moving in a circle with a constant angular speed. For
such a particle
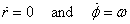
so the velocity is given as
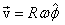
This is a well known result: the velocity of a particle
moving in a circle with a constant angular speed is in
the tangential direction and its magnitude is Rω.
How about the acceleration in polar coordinates? This
is the derivative of 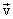 with
respect to time. Thus with
respect to time. Thus
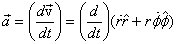
As was the case with the unit vector 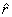 ,
the unit vector ,
the unit vector 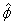 also
is a function of the polar angle Φ and as
such changes as the particle moves about. Thus in calculating
the acceleration, time derivative of also
is a function of the polar angle Φ and as
such changes as the particle moves about. Thus in calculating
the acceleration, time derivative of 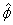 also
should be taken into account. From figure 4 it is clear
that also
should be taken into account. From figure 4 it is clear
that
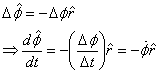
This can also be derived mathematically as

Using this derivative and the chain rule for differentiation,
we get
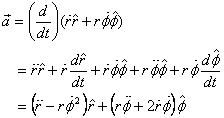
You can see that the expression
is a little complicated. The complexity of the expression
arises because the unit vectors are changing as the particle
moves. You can check for yourself that for a particle
moving with a constant velocity, the expression above
will give zero acceleration. Despite little complicated
expressions for the acceleration, employing polar coordinates
becomes really useful in situations where motion is circular-like
as we will see in two standard examples later. Let us
first go to one familiar example of a particle moving
in a circle for which r = R , 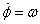 .
This gives .
This gives
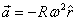
which is the correct answer for the centripetal acceleration.
For this reason 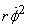 is
known as the centripetal term. Let us now solve an example
of mechanics using polar co-ordinates. is
known as the centripetal term. Let us now solve an example
of mechanics using polar co-ordinates.
|