Example 1: A pendulum in equilibrium as shown in figure 5. We show the coordinates of the bob in the figure 7 below.

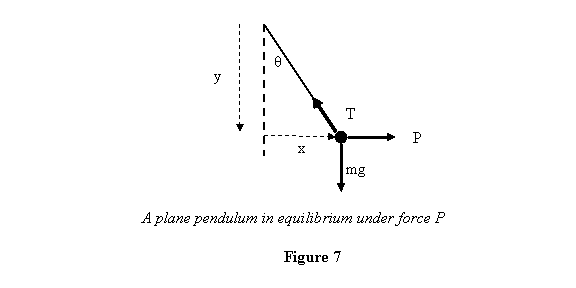
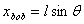
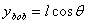
If the pendulum is give a virtual displacement i.e.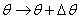

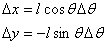
By the principle of virtual work, the total virtual work done by the external forces vanishes at equilibrium. So the equilibrium is described by

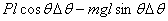
giving

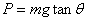
Which is the same answer as obtained earlier.

 

Example 2: This is the problem involving two crossed bars as shown in figure 2. We wish to calculate the force F required to keep the system in equilibrium using the principle of virtual work.

To apply the principle of virtual work, imagine a virtual displacement consistent with the constraint. The only displacement possible - because of only one degree of freedom - is that 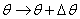. From figure 2 it is clear that the external forces on the system are F and 2mg (weight of the bars).

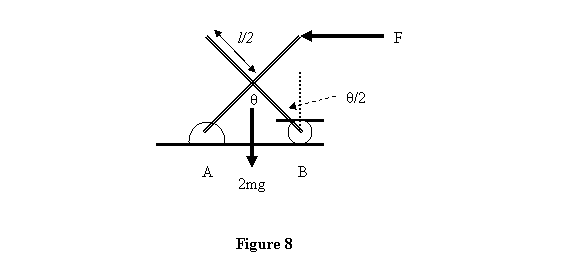
As θ increased to θ + Δθ , the point where the bars cross moves down by a distance (see figure 8)

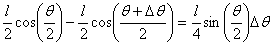
and the point when F is applied moves to the right by a distance

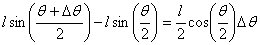
To calculate the net virtual work done, I remind you that work by a force 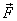is calculated by taking the dot product 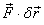, where 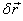represents the displacement of the point where the force is being applied. Thus the virtual work in the present case is

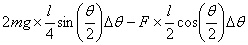
For equilibrium we equate this to zero to get

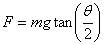
which is the same result as obtained earlier.

So you see in both these examples that by applying the method of virtual work, we have bypassed calculating the constraint forces completely and that is what makes the method easy to implement in large systems. The way to learn the method well is to practice as many problems as possible. I will now solve some examples to demonstrate the usefulness of the method for large system. To start with let us take the example which we gave in the beginning - that of toy with made with bars.

Example 3: If there are N crossings in the folding toy shown in figure 9, what is the force required to keep the system in equilibrium?

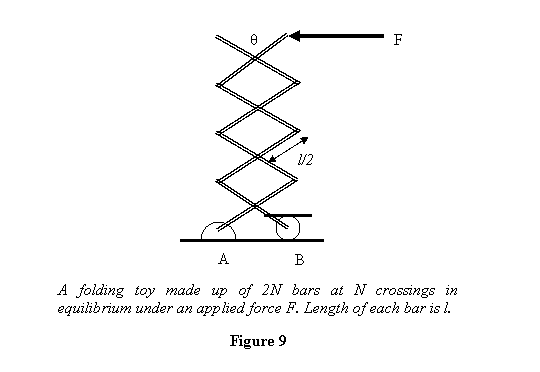
Again the degree of freedom = 1. The variable we use to describe the position of the mechanism is the angle between the bars i.e. θ. As the angle θ is changed to (θ+ Δθ), the upper end of the bar where force F is applied moves in the direction opposite to the force by

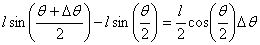
Thus the virtual work done by F is

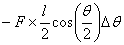
On the other hand, the first crossing moves down by

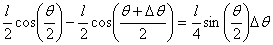
The second crossing by

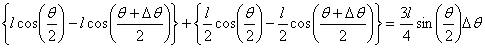
and the Nth crossing moves down by

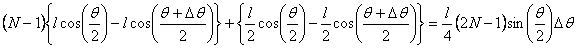All these displacements are in the same direction as the force = 2mg at each of the bar crossings. Thus the virtual work done by the weight of the mechanism is

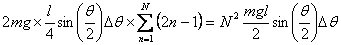
This gives a total virtual work done by the external forces to be

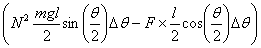
Equating this to zero for equilibrium gives

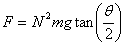
For N = 1 the answer matches with that obtained in the case of only two bars in example 2 above. For larger N , the force required to keep equilibrium goes up by a factor of N² .

Example 4: A 6m long electric pole of weight W starts falling to one side during rains. It is kept from falling by tying a strong rope at its centre of gravity (assumed to be right in the middle of the pole) and securing the other end of the rope on ground. All the relevant distances are given in figure 10. Assume that the lower end of the pole is like a pin joint. Under these conditions we want to find the tension in the rope using the method of virtual work.

 

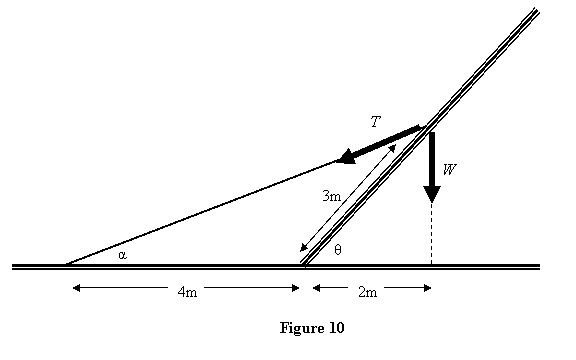
In this problem also there is only one degree of freedom θ. The constraint is that the pole can only rotate about the assumed pin joint at the ground. The constraint forces are the reactions at the ground and do no work on the pole when it rotates. There is also the constraint of the rigidity of the pole. Extend forces are W and T. By principle of virtual work when θ is changed to ( θ + Δ θ ) , the total virtual work vanishes. If the centre of gravity moves up by Δy and to the left by Δx as θ is increased to ( θ + Δθ ) , the virtual work done is

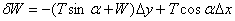
which, when equated to zero, gives

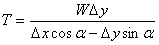
From the figure it is easy to see that

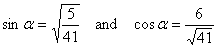
and (only the magnitude)

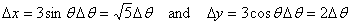
Substituting these in the expression for the tension gives

 

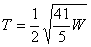
This concludes the lecture on the method of virtual work. In the lecture, I have given you an introduction to the method assuming that constraints do no work. The method is really useful when there are many constraints and the system is complicated. It makes calculations easier by avoiding calculating constraint forces. The method also provides basis for simplifying dynamics calculations under constrained motion. You will be learning more about it in an advanced course.