The following properties of the line integral of complex valued functions can be easily proved.
- If
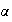 and
and 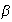 are complex numbers and if
are complex numbers and if 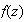 and
and 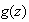 are (piecewise) continuous complex valued functions defined on a contour
are (piecewise) continuous complex valued functions defined on a contour 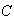 , then
, then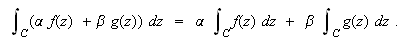
- Let
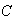 be a contour consists of a contour
be a contour consists of a contour 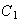 from
from 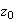 to
to 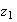 followed by a contour
followed by a contour 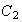 from
from 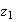 to
to 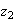 where the initial point of
where the initial point of 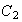 is the final point of
is the final point of 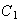 . It is denoted by the notation
. It is denoted by the notation 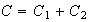 . If
. If 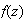 is a (piecewise) continuous complex valued function on
is a (piecewise) continuous complex valued function on 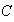 , then
, then 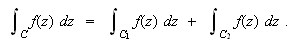
- If
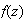 is a (piecewise) continuous complex valued function on a contour
is a (piecewise) continuous complex valued function on a contour 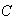 and if
and if 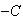 is the opposite curve to
is the opposite curve to 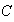 , then
, then 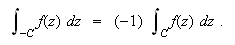
- f
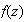 is a (piecewise) continuous complex valued function on a contour
is a (piecewise) continuous complex valued function on a contour 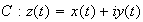 (
( 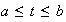 ), then
), then 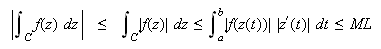 where
where 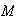 is an upper bound for the set
is an upper bound for the set 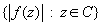 and
and 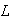 is the length of the contour
is the length of the contour 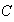 .
.