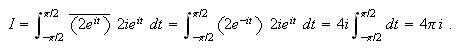Line Integrals or Contour Integrals: Suppose that ![]() for
for ![]() represent a contour (that is, piecewise smooth curve)
represent a contour (that is, piecewise smooth curve) ![]() , extending from a point
, extending from a point ![]() to a point
to a point ![]() . Let the function
. Let the function ![]() be defined on
be defined on ![]() . We define the line integral or contour integral of
. We define the line integral or contour integral of ![]() along the curve
along the curve ![]() as follows:
as follows:
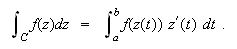
Example: Compute ![]() where
where ![]() is given by
is given by ![]() for
for ![]() .
.
Observe that ![]() for
for ![]() . Therefore,
. Therefore,