(vii) The function
is discontinuous at . To see this, let .
Then, . However, . Hence, does not exist.
5.2 .3
Theorem:
Let. Let be functions,both continuous at . Then the following holds:
(i) are continuous at .
(ii)If is defined in a neighbourhood of and is continuous at .
5.2 .4
Examples:
(i) It follows from the above theorem that every polynomial function 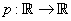with
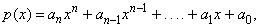
where 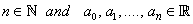is continuous. Also, any rational function , that is, a function of the form 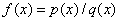where p and q are polynomial functions, is continuous at every point 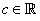for which .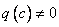
(ii) All trigonometric functions (and also, rational functions in them) are continuous wherever they are defined.
. To see this, let 
. 
. However, 
. Hence, 
does not exist.
. Let 
be functions,both continuous at 
. Then the following holds:
are continuous at 
is defined in a neighbourhood of 
and is continuous at 
with
is continuous. Also, any rational function , that is, a function of the form 
where p and q are polynomial functions, is continuous at every point 
for which 
.
with range 
. For 
, if 
is continuous at 
and 
is 
