(v) The function 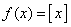 , is not continuous at c, if c is an integer since the left hand limit is not equal to the
right hand limit.
(vi) Consider the function 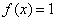 if x is rational, and 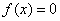 if x is irrational. It is discontinuous at every
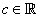 . To see this note that given 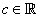 , we can choose 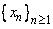 and 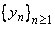 both conveying to c, where each 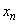 is a rational an each 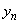 is an irrational. Then, 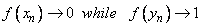 . Thus,
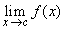 does not exist. |