Recall that for a function 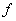, which may or may not be defined at a point c , if 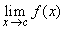exists, then it is the value that the function 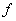is expected to take in consideration of its values at points in a neighborhood of c. Suppose, the function is actually defined at c . In case the value expected of the function at x = c exists and is equal to the actual value 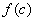, it is natural to say that there is a continuity in the behaviour of 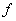. This motivates our next definition.
5.2.1
Definition:
Let and be an interior point of . We say is continuous at if exists and is equal to
. Equivalently is continuous at c if for every , there is such that
.
We say is continuous on if is continuous at each . If we say that is continuous at if
exists and is equal to , and is continuous at b if exists and is equal to .
5.2.2
Examples:
(i) The function is continuous at every point. For example we can take , for any given to
claim that .
(ii) The function is continuous everywhere as , and hence once again we can choose to claim that .
, which may or may not be defined at a point c , if 
exists, then it is the value that the function 
, it is natural to say that there is a continuity in the behaviour of 
and 
be an interior point of 
. We say 
, there is 
such that 
. 
. If 
we say 
if
exists and is equal to 
, and 
exists and is equal to 
. 
is continuous at every point. For example we can take 
, for any given 
to 
.
is continuous everywhere as 
, and hence once again we can choose 
