Suppose 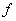 has a local maximum at has a local maximum at 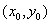 . Then, we can find some . Then, we can find some 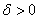 such
that such
that
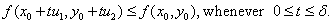
Hence, if 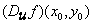 exists, then exists, then
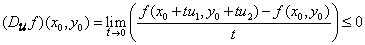
Similarly, 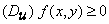 . Hence, . Hence, 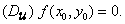
The case of a local minimum is similar. This proves (i). To prove (ii), we note that if 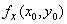 exists and if exists and if 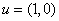 , then , then
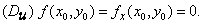
Considering 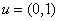 , we similarly obtain , we similarly obtain 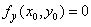 . .
|