Let
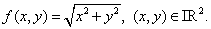
Then, 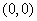 is the only critical point of is the only critical point of 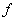 , as both , as both 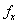 and and 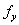 do not exist at do not exist at 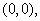 and at every other point both exist are non-zero. The point and at every other point both exist are non-zero. The point 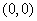 is obviously a point of local minimum, with local minimum being is obviously a point of local minimum, with local minimum being 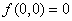 . Thus, the condition in theorem . Thus, the condition in theorem 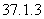 is only necessary, not sufficient. is only necessary, not sufficient. |