Let
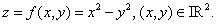
Then, both 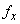 and and 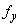 exist at every point exist at every point 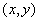 and and
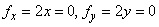 , ,
imply that 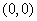 is the only cortical point. But at is the only cortical point. But at 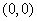 , , 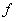 has no local maximum for has no local maximum for
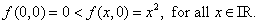
Also, 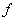 does not have a local at minimum at does not have a local at minimum at 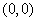 since since
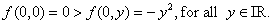
Thus, in other words, in every neighborhood of 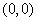 , there is a curve in the domain at every point of which , there is a curve in the domain at every point of which 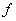 takes value bigger than takes value bigger than 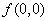 , and also there exists another curve in the domain of , and also there exists another curve in the domain of 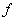 at every point of which at every point of which 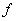 takes value less than takes value less than 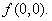 |