| |
i.e. the Fermi level lies in the middle of the forbidden gap . Note that there is no contradiction with the fact that no state exists in the gap as 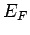 is only an energy level and not a state. is only an energy level and not a state. |
| |
By substituting the above expression for Fermi energy in (A) or (B), we obtain an expression for the number density of electrons or holes ( 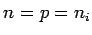 ) ) |
| |
where 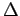 is the width of the gap. is the width of the gap. |