|
permittivity of the free space 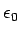 is replaced by is replaced by  , the permittivity of the medium (silicon). , the permittivity of the medium (silicon). |
|
free electron mass being replaced by the effective mass of the donor electron. |
| |
Recalling that the energy of an electron in the the hydrogen atom is given by |
| |
where 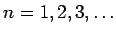 , we need to replace , we need to replace 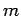 by by 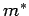 and and 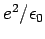 by by 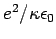 , where , where 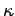 is the relative dielectric constant of the medium. Using is the relative dielectric constant of the medium. Using 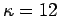 for Si and for Si and 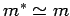 , the free electron mass, the ionization energy of the electron bound to the donor atom is , the free electron mass, the ionization energy of the electron bound to the donor atom is 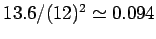 eV, if the electron is in the ground state. Thus the donor energy level lies close to the bottom of the conduction band. In case of semiconductors, the donor ionization energy is defined as the energy required to elevate the donor electron to the conduction band. eV, if the electron is in the ground state. Thus the donor energy level lies close to the bottom of the conduction band. In case of semiconductors, the donor ionization energy is defined as the energy required to elevate the donor electron to the conduction band. |