 |
Consider the surface integral from the six faces individually. For the face AEOD, the normal is along 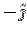 . On this face . On this face 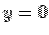 so that so that 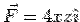 . Since . Since 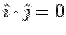 , the integrand is zero. For the surface BFGC, the normal is along , the integrand is zero. For the surface BFGC, the normal is along 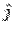 and on this face and on this face 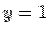 . On this face the vector field is . On this face the vector field is 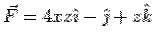 . The surface integral is . The surface integral is
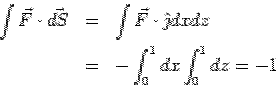
|