 |
Consider the top face (ABFE) for which the normal is 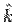 so that the surface integral is so that the surface integral is 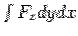 . On this face . On this face 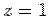 and and 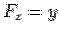 . The contribution to the surface integral from this face is . The contribution to the surface integral from this face is
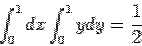
For the bottom face (DOGC) the normal is along 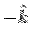 and and 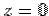 . This gives . This gives 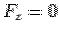 so that the integral vanishes. so that the integral vanishes.
For the face EFGO the normal is along 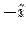 so that the surface integral is so that the surface integral is 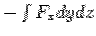 . On this face . On this face 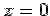 giving giving 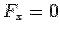 . The surface integral is zero. For the front face ABCD, the normal is along . The surface integral is zero. For the front face ABCD, the normal is along 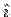 and on this face and on this face 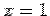 giving giving 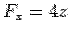 . The surface integral is . The surface integral is
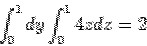
Adding the six contributions above, the surface integral is 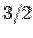 consistent with the divergence theorem. consistent with the divergence theorem. |