 |
Example 17 :
A vector field is given by 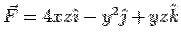 . Find the surface integral of the field from the surfaces of a unit cube bounded by planes . Find the surface integral of the field from the surfaces of a unit cube bounded by planes 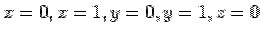 and and 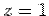 . Verify that the result agrees with the divergence theorem. . Verify that the result agrees with the divergence theorem.
Solution :
Divergence of 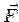 is is
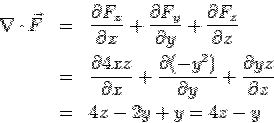
The volume integral of above is
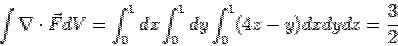
|