| |
We can generalize the above to closely packed volumes and conclude that the flux out of the bounding surface 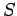 of a volume of a volume 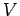 is equal to the sum of fluxes out of the elemental cubes. If is equal to the sum of fluxes out of the elemental cubes. If 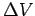 is the volume of an elemental cube with is the volume of an elemental cube with 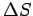 as the surface, then, as the surface, then, |
| |
The quantity in the bracket of the above expression was defined as the divergence of 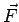 , giving , giving |
| |
This is known as the Divergence Theorem. |
| |
We now calculate the divergence of 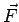 from an infinitisimal volume over which variation of from an infinitisimal volume over which variation of 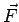 is small so that one can retain only the first order term in a Taylor expansion. Let the dimensions of the volume element be is small so that one can retain only the first order term in a Taylor expansion. Let the dimensions of the volume element be 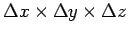 and let the element be oriented parallel to the axes. and let the element be oriented parallel to the axes. |
| |
Consider the contribution to the flux from the two shaded faces. On these faces, the normal is along the 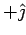 and and 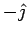 directions so that the contribution to the flux is from the y-component of directions so that the contribution to the flux is from the y-component of 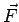 only and is given by only and is given by |