| |
The line integral of 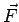 can then be written as follows : can then be written as follows : |
| |
where the symbols 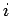 and and 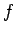 represent the initial and thec final positions and in the last step we have used an expression for represent the initial and thec final positions and in the last step we have used an expression for 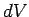 similar to that derived for similar to that derived for 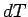 above. Thus the line integral of the force field is independent of the path connecting the initial and final points. If the initial and final points are the same, i.e., if the particle is taken through a closed loop under the force field, we have above. Thus the line integral of the force field is independent of the path connecting the initial and final points. If the initial and final points are the same, i.e., if the particle is taken through a closed loop under the force field, we have |
| |
Since the scalar product of force with displacement is equal to the work done by a force, the above is a statement of conservation of mechanical energy. Because of this reason, forces for which one can define a potential function are called conservative forces. |