| |
Note that the change 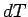 involves a change in temperature with respect to each of the three directions. We define a vector called the gradient of involves a change in temperature with respect to each of the three directions. We define a vector called the gradient of 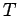 , denoted by , denoted by 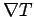 or grad or grad 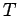 as as |
| |
Note that 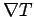 , the gradient of a scalar , the gradient of a scalar 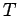 is itself a vector. If is itself a vector. If 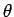 is the angle between the direction of is the angle between the direction of 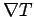 and and 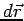 , , |
| |
where  is the component of the gradient in the direction of is the component of the gradient in the direction of 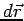 . If . If 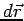 lies on an isothermal surface then lies on an isothermal surface then 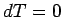 . Thus, . Thus, 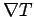 is perpendicular to the surfaces of constant is perpendicular to the surfaces of constant 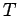 . When . When 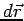 and and 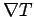 are parallel, are parallel, 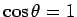 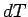 has maximum value. Thus the magnitude of the gradient is equal to the maximum rate of change of has maximum value. Thus the magnitude of the gradient is equal to the maximum rate of change of 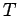 and its direction is along the direction of greatest change. and its direction is along the direction of greatest change. |
| |
The above discussion is true for any scalar field 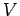 . If a vector field can be written as a gradient of some some scalar function, the latter is called the potential of the vector field. This fact is of importance in defining a conservative field of force in mechanics. Suppose we have a force field . If a vector field can be written as a gradient of some some scalar function, the latter is called the potential of the vector field. This fact is of importance in defining a conservative field of force in mechanics. Suppose we have a force field 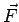 which is expressible as a gradient which is expressible as a gradient |