From the orbitals, wavefunctions can be constructed using equation (6.2). The square of the wavefunction gives the probability of finding electrons in the corresponding volume elements.
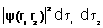 gives the probability of finding electron 1 in volume element gives the probability of finding electron 1 in volume element
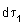 at r1 and electron 2 in volume element at r1 and electron 2 in volume element
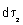 at r2. Since atoms are spherically symmetrical, it is better to consider the radial probability density at r2. Since atoms are spherically symmetrical, it is better to consider the radial probability density
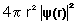 where where 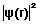 is the probability density of finding any one electron at r . The plot for lithium atom is shown below. is the probability density of finding any one electron at r . The plot for lithium atom is shown below. |