For a multielectron atom such as He, Li, etc. the Schrödinger equation may be written as H
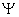 = E = E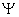 where H is the operator representing the kinetic and potential energies of
all the particles and where H is the operator representing the kinetic and potential energies of
all the particles and 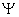 and E are the wavefunction and energy respectively. For a helium atom, keeping the nucleus fixed (this is not a bad approximation since the nuclei are much heavier than the electrons) H can be written as and E are the wavefunction and energy respectively. For a helium atom, keeping the nucleus fixed (this is not a bad approximation since the nuclei are much heavier than the electrons) H can be written as |